Introduction and motivation
This RFC is the third set of optimizations to enhance quantized convolution on Arm architectures. To give a brief summary:
- Basic Armv8-A convolution implementation (through gemm): [RFC] Improve quantized convolution performance for armv8 architectures
- Dot product enhancements for Armv8.2-A: [RFC] Accelerate quantized convolution through dot-product
In this RFC we will support the Matrix Multiply Accumulate instruction. : https://developer.arm.com/docs/ddi0602/g/simd-and-floating-point-instructions-alphabetic-order/smmla-vector-signed-8-bit-integer-matrix-multiply-accumulate-vector
This instruction is optionally supported from Armv8.2-A onward, while it is mandatory from Armv8.6-A onward.
Overview of the Matrix Multiply Instruction
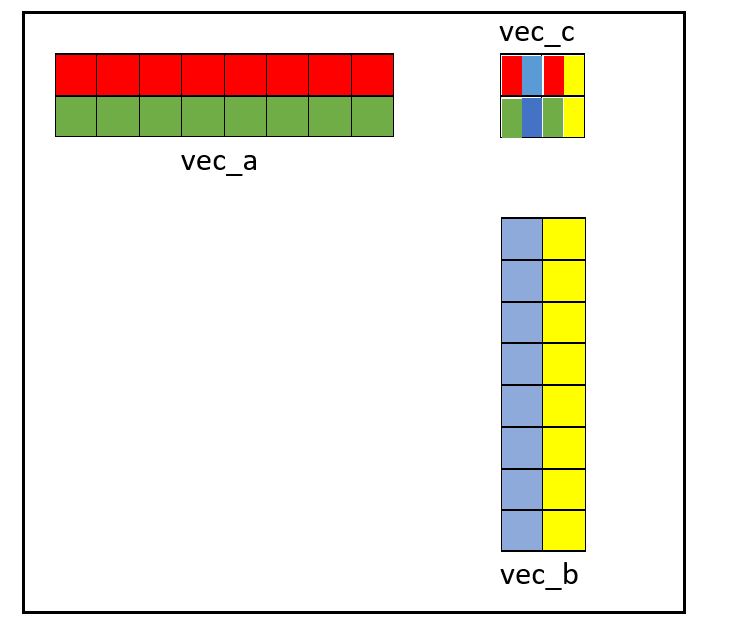
Let’s have a brief introduction of how smmla works. While we will add support for ummla as well, for the remaining of this RFC we will only mention its signed version.
The following picture briefly shows how smmla works:
In the picture, vec_a and vec_b are int8x16 (or .16b) registers while vec_c is a int32x4 (or .4s) register. You may notice that this is quite different from dot-product. In dot-product we compute a 1x4 sub-row of the output tile. With smmla, we compute a 2D 2x2 sub-tile of the final result. This will need proper handling during the tiling phase of the algorithm
GEMM implementation through smmla
Now that we have enough understanding of how smmla works, we can discuss how we decided to add support for it.
Let’s reiterate once more how the general GEMM algorithm (C=A*B) works:
- Subdivide matrix
Ain adjacent tiles (a process called packing or interleaving) - Interleave and transpose matrix
B(this can be done offline) - Run GEMM to produce a
C_interleavedversion of the output - Unpack
C_interleavedto obtainC
The tiling is usually chosen to maximize the register utilization. In this case, the best tiling to exploit register allocation is still a 8x12 tile (like the one we used for dot-product). The difficulty with smmla is that C_interleaved (i.e., the tiled version of the output) will be composed by 2x2 sub-tiles that need to be extracted when unpacking. The following picture tries to show the situation:
Please note that A_tile and B_tile (and thus C_tile as well) are shown in their native layout. The problem is that the four elements of each sub-tile generated (e.g., the red 2x2 sub-tile) are contiguous in memory. This needs to be expressed at compute level in order to then unpack properly.
The compute node
Given what stated above, the final compute node to produce C_interleaved and unpack the result is the following:
C_interleaved = te.compute((batches, M_padded // tile_rows_A, N_transformed, 4, 6, 2, 2),
lambda b, x, y, w, z, s, t: te.sum(
A_interleaved[b, x, k // tile_cols_A, 2 * w + s, idxm(k, tile_cols_A)].astype("int32") *
B_interleaved_t[y, k // tile_cols_B, 2 * z + t, idxm(k, tile_cols_B)].astype("int32"),
axis=k,),
name="C_interleaved",)
C = te.compute((batches, M, N),
lambda b, x, y: C_interleaved[
b,
x // tile_rows_A,
y // tile_rows_B,
idxm(x, tile_rows_A) // 2,
idxm(y, tile_rows_B) // 2,
idxm(idxm(x, tile_rows_A), 2),
idxm(idxm(y, tile_rows_B), 2),
].astype(out_dtype),
name="C",)
We are simply expressing during the computation that the output 8x12 tile is really a 4x6x2x2 tile (i.e., it is a 8x12 tile, composed by 2x2 sub-tiles). This is also taken into account when we are unpacking C_interleaved.
The tensorization rule
Once we have our C_interleaved in the right form, it is fairly simple to tensorize on the inner 2x2 sub-tile and unroll the outer dimensions to have a final 8x12 output tile.
The following snippet of code is an extract of the tensorization rule we are using
vec_a = ins[0].vload([0, 0], dtype_vec)
# Load in vec_b the two rows of B
# vec_b = [0, 2, 4, 6, 8, 10, 12, 14;
# 1, 3, 5, 7, 9, 11, 13, 14,]
vec_b = ins[1].vload([0, 0], dtype_vec)
# Execute the matrix multiplication via (s/u)mmla:
# vec_c = [a*0 + b*2 + c*4 + d*6 +e*8 + f*10 + g*12 + h*14;
# a*1 + b*3 + c*5 + d*7 +e*9 + f*11 + g*13 + h*15;
# i*0 + j*2 + k*4 + l*6 +m*8 + n*10 + o*12 + p*14;
# i*1 + j*3 + k*5 + l*7 +m*9 + n*11 + o*13 + p*15]
vec_c = outs[0].vload([0, 0], "int32x4")
vmmla = tvm.tir.call_llvm_intrin(
"int32x4", llvm_intrin, tvm.tir.const(3, "uint32"), vec_c, vec_a, vec_b,
)
# Store the result
ib.emit(outs[0].vstore([0, 0], vmmla))
This is very close to the previous picture where we showed the smmla functioning. It is also instructive to show how we use the intrinsic within the schedule:
mmla = mmla_2x2_int8_int8_int32(in_type)
xi_inner, yi_inner = C_interleaved.op.axis[5:7]
k_outer, k_inner = s[C_interleaved].split(k, 8)
s[C_interleaved].reorder(
b_outer_gemm_fused, inner_gemm, k_outer, xi, yi, xi_inner, yi_inner, k_inner
)
s[C_interleaved].tensorize(xi_inner, mmla)
s[C_interleaved].unroll(xi)
s[C_interleaved].unroll(yi)
Other then splitting the reduction axis in 8 (i.e., the reduction dimension of mmla), we can simply apply the intrinsic and unroll the outer tile dimensions.
Testing and performance
While this instruction is not yet supported by real hardware, at Arm we have been able to run and verify this instruction on internal cycle-accurate simulator. We saw for instance, on a [75x75x80] * [3x3x80x192] convolution (heaviest layer from inceptionV3), a 35% improvement compared to the dot-product implementation.
PR
The PR for this RFC is available here: https://github.com/apache/incubator-tvm/pull/6802