Motivation
In recent RFCs we successfully boosted convolution performance on native Armv8-A architectures. When using Armv8.2-A and above ISAs, developers are provided with a richer set of instructions, among which the dot-product instruction udot (or sdot) can be particularly useful for Machine Learning applications (as a reference, see the Neoverse optimization guide).
Basic udot/sdot functioning
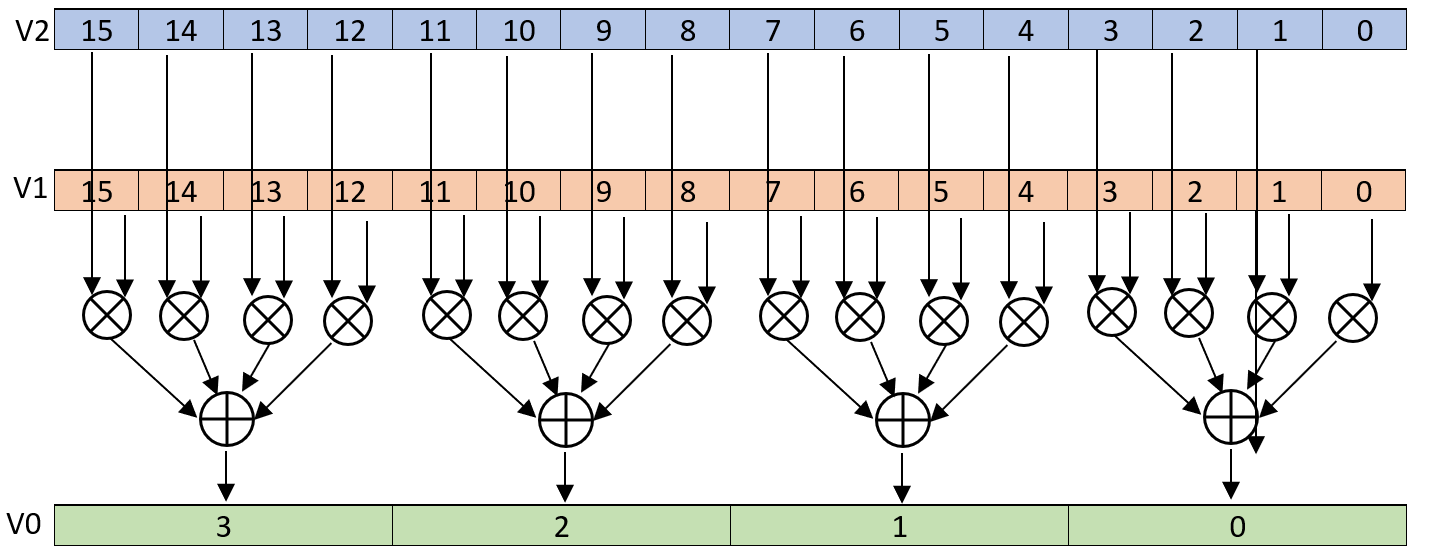
The instruction
udot v0.4s, v1.16b, v2.16b
Subdivides the registers v1 and v2 in blocks of 4 uint8 elements and places their dot-product into the corresponding 32bit word in v0. You can see this operation depicted in the following picture:
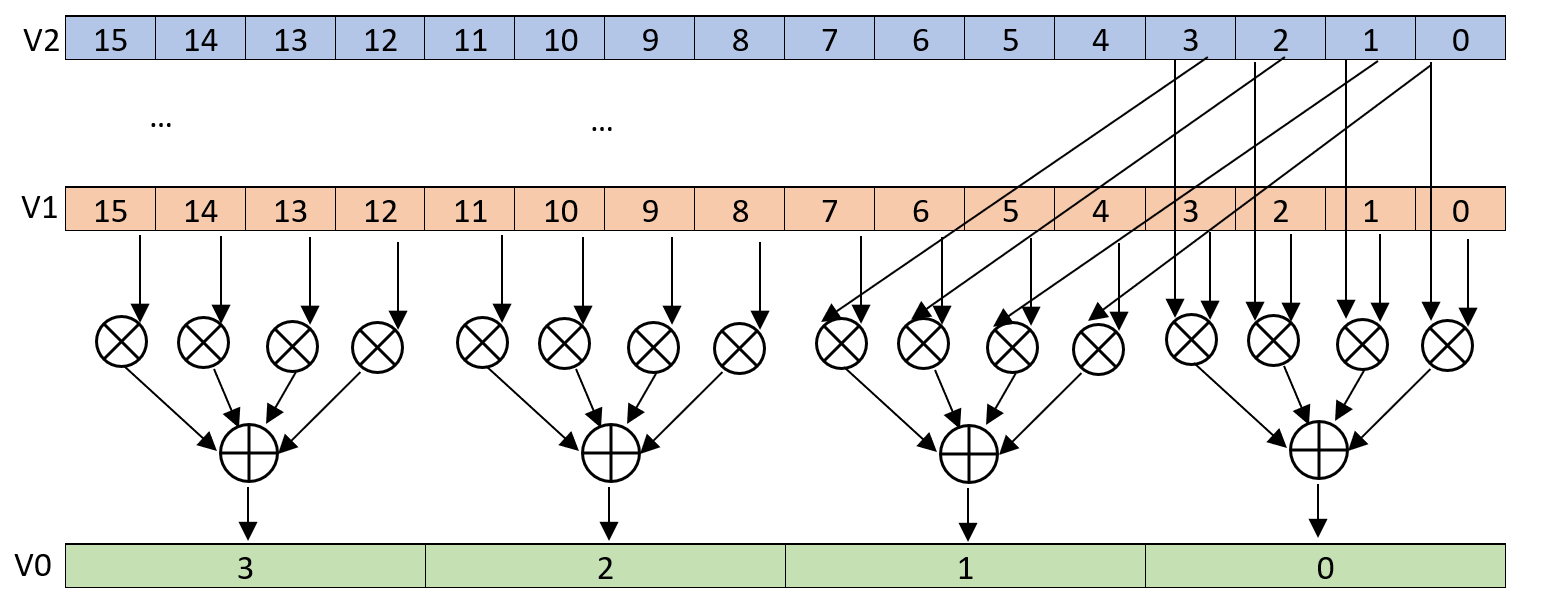
Another less known version of this instruction is the indexed dot-product:
udot v0.4s, v1.16b, v2.16b[0]
This instruction is taking the first 4 uint8 elements of vector v2 and producing the dot-product with each groups of 4 elements from vector v1. This is depicted in the following picture:
This last version is the one we will use through the remaining of this RFC.
Implementation strategy
We decided to add dot-product support through two intrinsics and to exploit those intrinsics through tensorization. Differently from the previous intrinsic for Armv8-A (which was written through inline assembly), we have been able to write them entirely through TIR/LLVM instructions. The main difference is that, given two tiles tile_A and tile_B the output tile_C produced with the dot-product is partial but correct. In the case of Armv8-A, instead, we needed some additional assembly magic (i.e., addp instructions) to produce the correct partial tile.
Strategy #1: 8x12 output tile, A interleaved and B transposed and interleaved
In this case the approach is very similar to the Armv8-A RFC.
Interleave A: We interleave (and pad if necessary) the rows of A in blocks of 8x4. This means that each tile will contain 4 consecutive elements of 8 rows of A.
Interleave and transpose B: We block transpose B as in Armv8-A RFC. In this case though, we use blocks of 12x4. Each tile of the reshaped B will contain 4 consecutive elements of 12 columns of B
Computation through dot-product: We use an mmla4x4 intrinsic in order to produce a 4x4 (interleaved) tile given 4x4 tiles from A and B. Please note that we will unroll it by two, in order to produce the correct 8x4 output tile.
This is the rule we are using:
vec_a = ins[0].vload([0, 0], dtype_vec) # Now vec_a contains 4 rows of A (4 elements each)
vec_aa = [select_word(vec_a, i, dtype_vec) for i in range(0, 4)] # Select the i-th row
vec_b = ins[1].vload([0, 0], dtype_vec) # vec_b contains the 4 columns of B (4 elements each)
# Execute the matrix multiplication
for i in range(0, 4):
vec_c = outs[0].vload([i, 0], 'int32x4')
vdot = tvm.tir.call_llvm_intrin(
'int32x4',
'llvm.aarch64.neon.sdot',
tvm.tir.const(3, 'uint32'),
vec_c, vec_b, vec_aa[i])
# Store the result
ib.emit(outs[0].vstore([i, 0], vdot))
We will give some more information about select_word later in this RFC
Strategy #2: 4x16 output tile, A native and B transposed and interleaved
This strategy is different from the one we previously adopted, and deserves some more explanation.
A is in native form: We don’t interleave A, but we do pad it if necessary. Now the i-th load instruction is loading 16 elements from the i-th row of A
Interleave and transpose B: For B nothing changes. We tile in the same way we did previously, but with a different 16x4 tile shape. Each tile of the reshaped B will contain 4 consecutive elements of 16 columns of B
Computation through dot-product: We use an mmla16x4 intrinsic. The inputs are a Rx4 tile of A (R is the number of resulting rows) and a 16x4 tile of B. Before showing any code, we provide the tiled computation in the following picture, where R is set to 4. The idea is the following:
- A single load reads 16 consecutive elements from matrix
A(which is in its native form). 4 of them are green, 4 of them are blue and so on - The first output row C[0,0:4] is produced in the following way:
`C[0, 0:4] = A[0,0:4] *B_interleaved_t[0:4,0:4]`
`C[0, 0:4] += A[0,4:8] *B_interleaved_t[4:8,0:4]`
`C[0, 0:4] += A[0,8:12] *B_interleaved_t[8:12,0:4]`
`C[0, 0:4] += A[0,12:16] *B_interleaved_t[12:16,0:4]`
- Repeat the same operation for each the
Rrows of C
Few things worth underlying:
- In the picture we tried to render the algorithm with different colors: multiplications only happen between tiles of same colors
- The tiles of
B-interleaved_tin the picture do not represent the real memory layout. Basically tile[0,0]is stored by rows, followed by tile[1,0],[2,0],[3,0],[0, 1], etc… (this reinforces the fact thatB_interleaved_tis a block transposed version ofB) - Very importantly, the output C is already in its native form. We thus don’t need to unpack it
For completeness we write down the tensorization node we use to implement the above tiled computation:
for k in range(0, rows):
vec_a = ins[0].vload([k, 0], dtype_vec)
for j in range(0, 4):
for i in range(0, 4):
vec_aa = select_word(vec_a, i, dtype_vec)
vec_b = ins[1].vload([i, 4*j, 0], dtype_vec)
vec_c = outs[0].vload([k, 4*j], 'int32x4')
vdot = tvm.tir.call_llvm_intrin(
'int32x4',
'llvm.aarch64.neon.sdot',
tvm.tir.const(3, 'uint32'),
vec_c, vec_b, vec_aa)
How to produce the correct indexed dot-product: select_word() function:
The indexed dot-product is not available as an LLVM intrinsic. It is instead produced as a LLVM/IR optimization when we do:
# Reinterpret vec_a as 4 int32 words
vec_int32 = tvm.tir.call_intrin('int32x4', 'tir.reinterpret', vec)
# Broadcast the lane-th word
vec_int32_shuffled = tvm.tir.Shuffle([vec_int32], [lane, lane, lane, lane])
# Convert back to uint8x16
vec_int8_broadcast = tvm.tir.call_intrin(dtype_vec, 'tir.reinterpret', vec_int32_shuffled)
udot(vec_c, vec_b, vec_int8_broadcast)
The first 3 instructions are implemented in a utility function named select_word in topi/arm_cpu/tensor_intrin.py
Why implementing both strategies?
If we run some math, we can see that the number of memory accesses in the case of the interleaved approach is slightly smaller compared to the hybrid approach. However, the idea is that the hybrid kernels don’t need interleaving of data and un-interleaving of the output. Since we try to fuse those transformations it is not entirely clear which one is best. The best approach is to let the tuner decide the winner
Performance improvements
In order to initially test performance improvements, we consider again inception_V3 (which is a good benchmark, given its shape variety) running on a Neoverse N1 machine.
The results we measured are as follows:
- 2.41x improvement compared to the Armv8-A implementation
- About 5% slower than ArmNN (which uses ACL under the hood)
These are encouraging results which is why we will submit this improvement as is, before adventuring in more exotic optimizations.
Next steps
Comparing performance across different networks
While the results for inception_v3 were satisfactory, we will compare performance for other networks against ArmNN. This is to understand if there are big gaps that need to be considered.
Improving performance further: padding and fusion
The hybrid strategy aims at avoiding memory-bound operations (like packing/unpacking) and gives us the possibility to fuse the requantization directly during the main computation. However, we ran into the following issues:
-
Since we are applying the
mmla16x4intrinsic through tensorization, we need to padAbeforehand which is actually a memory-bound operation, defeating the benefits given by this approach. Simple approaches to remove padding seem ineffective:- If we don’t pad and run tensorize over a variable dimension tiles, it simply fails (see this discuss post)
- If we don’t pad and run tensorize only over fixed dimension tiles,
@tir.likelystatements appear hitting performance.
-
For the same reason we cannot fuse the requantization during the computation. In addition to the inability to
compute_atwithin tensorize, we are also blocked by the inability tocompute_aton fused/split axis (as mentioned in this post)
We are currently working to find a well designed solution in order to address both the issues. Possible solutions are still being evaluated and every suggestion is welcome!
PR
The PR for this RFC is available here: https://github.com/apache/incubator-tvm/pull/6445