Intruduction
In this document, we propose a design to lower DistIR, a logical unified distirbuted IR, to ranked physical single-device Relax IRs that is ready to be consumed by the current TVM compiler infrastructure. After compiling the ranked Relax IR, the compiled executable is ready to be exeucted by a runtime, such as Relax VM and Disco, in a distributed way.
We also point out that some of the design choices made by DistIR and Disco may miss potential optimization oppourtunities and cause extra complexity when it comes to irregular sharding.
Motivation
For cloud foundational model providers, being able to execute inference in a distributed way is important to guarantee the SLA(especially latency), as well as efficiency.
We at Kwai AI Platform Compiler Group are working on compiling foundational models with TVM-Unity and MLC-LLM, and we noticed that there’s still a gap between high-level DistIR and low-level single-device Relax IR. We also seen multiple questions and issues raised by community regarding this direction.
Hence, we aim to propose a design that connects DistIR and low-level infrastructures provided by TVM, which enables it to support distributed inference.
Related Work in Community
DistIR
A Relax dialect that describes logical distributed sharding strategies. DistIR also provides infrastructure to propagate sharding information just like GSPMD. DistIR represents sharding strategy through DTensor and device mesh, which is expressive enough for DP, TP and PP. There exists abstraction redundancy in GSPMD where “partially tiled tensor” is just a special case of “tiled tensor”, DistIR unified them together hence eliminates this redundancy.
Disco
A Framework-Agnostic SPMD Runtime for Distributed Inference/Training. It is a single-controller system which consists of a controller and a group of workers, the controller broadcasts commands to all workers who then executes the commands. The single-controller architecture provides tremendous programmability because it enables programmers to write distributed code just like centralized code.
Challenges
There’re two challenges in lowering DistIR to single-device Relax IRs.
C1: Irregular sharding
Both DistIR and Disco adopt SPMD paradigm. However, when it comes to irregular sharding, execution differs naturally on different devices, the complexity must be resolved at some level.
We argue that it is beneficial to represent this difference in IR explicitly instead of hidding it, which eventually shifts the complexity to some lower-level components, such as runtime, and cause extra complexities and miss potential optimization opportunities.
We give two examples to demonstrate it.
1. Tail Block
First, in the code snippet below, the ‘M’ axis of the ‘matmul’ is split to two devices. Notice that tensor A and C’s shapes differ at device 0 and 1. With a single program, or say IR, we are unable to represent this difference.
@I.ir_module
class ShardingAlongReductionAxis:
I.module_attrs({"device_num": 2})
I.module_global_infos({"mesh": [R.device_mesh((2,), I.Range(0, 2))]})
# Represents sharding stategy with DTensor and remove 'annotate_sharding' op.
@R.function
def foo(
A: R.DTensor((127, 128), "float32", "mesh[0]", "S[1]"),
B: R.DTensor((128, 128), "float32", "mesh[0]", "S[0]"),
) -> R.DTensor((127, 128), "float32", "mesh[0]", "R"):
C: R.DTensor((127, 128), "float32", "mesh[0]", "R") = R.matmul(A, B, out_dtype="void")
return C
Applying padding is a possible way to resolve this differece, however, padding is asymmetric on devices, in this example, device 0 does not require padding but device 1 does. A new ‘asymmetric_pad’ op is needed, this is what we emphasized earlier as ‘shifting complexity to other lower level components’.
On the other hand, padding wastes extra computation and memory resources, hence miss potential optimization oppourtunities.
2. Sharding Spatial Axis of Slinding Window Operaions
Another example is sharding spatial axis of operations such as CONV and POOL. In this case, each device’s input tensor shard is overlapped, which requires extra asymmetric communications among each other. Again, we can certainly add new op to support this type of irregular communication, but this makes the list of ops longer and longer, and analysis and optimization upon it is more difficult.
C2: Abstraction leak in DistIR
In DistIR, there’re two kinds of sharding, R, which stands for Replicate, and S, which stands for non-overlapped Sharding. However, neither of them can represent sharding along reduction axis.
For example, in the following code snippet, the ‘K’ axis of the ‘matmul’ is splited to two devices, currently DistIR use ‘R’ to represent the result matrix C, which gives the ‘matmul’ a implicit ‘AllReduce’ epilogue. This will cause two problems:
-
First, it forces the ‘allreduce’ to be exeucted right after the ‘matmul’, which potentially miss some optimization oppourtunities.
For example, a ‘relu’ followed by the ‘matmul’ could not be fused because of the implicit ‘allreduce’.
-
Second, implicity make analysis and lowering more difficult.
For the ‘relu’ example above, we can certainly develop optimization passes that identify the pattern and fuse it, but this introduces extra complexity and makes pass developer’s life harder.
@I.ir_module
class ShardingAlongReductionAxis:
I.module_attrs({"device_num": 2})
I.module_global_infos({"mesh": [R.device_mesh((2,), I.Range(0, 2))]})
# Represents sharding stategy with DTensor and remove 'annotate_sharding' op.
@R.function
def foo(
A: R.DTensor((128, 128), "float32", "mesh[0]", "S[1]"),
B: R.DTensor((128, 128), "float32", "mesh[0]", "S[0]"),
) -> R.DTensor((128, 128), "float32", "mesh[0]", "R"):
C: R.DTensor((128, 128), "float32", "mesh[0]", "R") = R.matmul(A, B, out_dtype="void")
return C
Proposed Design
To solve the challenges mentioned before, we poposed our design as following.
Overall Architecture
Ranked Relax IR & VM Executable
The core concept in this design is Ranked Relax IRModule and Ranked Relax VM Executable, which are the distributed counterparts of the current single-device version. Ranked means we use independant IR/executable for each unique rank(or device) in the communication group(device mesh). Note that we only allocate IR/executable for unique ranks, if multiple ranks has exactly the same structure, they will share the same IR/executable. Hence, our design is basiclly an example of MPMD paradigm.
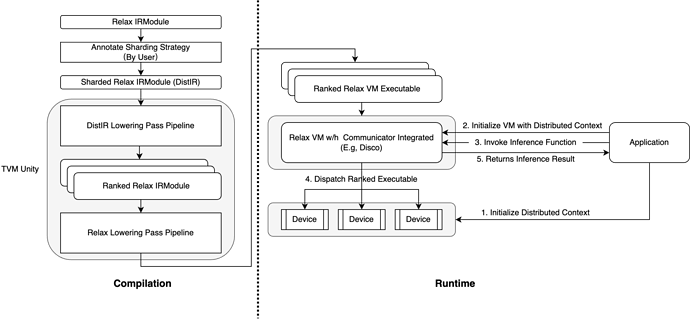
Compilatin phase
Users first annotate their desired sharding stratgy, we then reuse DistIR’s ShardingPropagation pass to propagate the sharding startegy to the entire graph. We then run a series of DistIR lowering passes, which will be explained in later chapter, to split the logical unified DistIR to ranked physical single-device Relax IR that is ready to be consumed by TVM compiler infrastructure. Note that if all ranks are exactly the same, the lowered Ranked Relax IRModule contains only a single common IR. Finally, each ranked IR is compiled with current TVM compiler infrastructure to produce the final Ranked Relax VM Executable.
Runtime phase
User first initialize their desired distributed context(e.g, through Disco’s Session object), this will assign a unique rank id for each device. Then, user can invoke inference function call and the VM needs to dispatch to the right function in Ranked Relax VM Executable according to device’s rank. Finally, necessary synchronization should be done(e.g, using Disco’s SyncDevice function) and the result is returned to user.
Introduce Sharding Type ‘I’
To resolve C2, we introduce a new sharding type ‘I’, which stands for intermediate tensor that is waiting to be reduces, to explicitly express reduction semantics.
‘I’ may contain mutiple subtypes to represent different reduction types, including ‘I_SUM’, ‘I_MEAN’, ‘I_MIN’, ‘I_MAX’. Note that the subtype could also be implemented as an op attribute. Examples and advantages of introducing this new type is elaborated in section Example 3
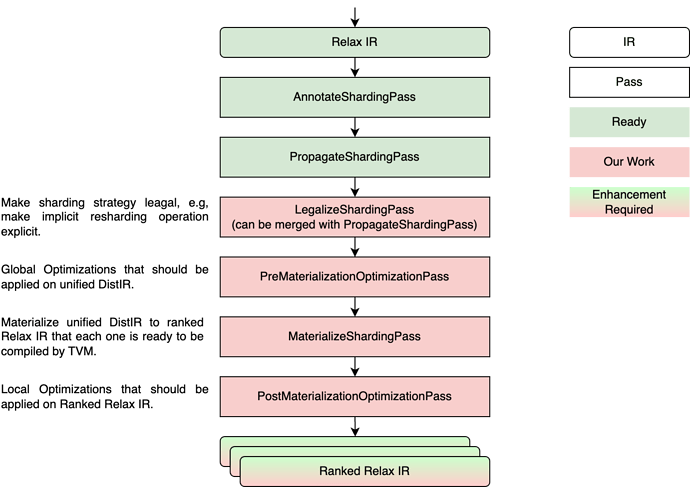
Compilation Pipeline
In this part, we introduce our main design, the compilation pipeline. The overall pipeline is shown in the image below. We will introduce each pass through an example IR.
Input Relax IR
We will use the following example to demonstarte how the pipeline works.
@I.ir_module
class LoweringDistIRExampleModule:
@R.function
def foo(
x: R.Tensor((127, 128), "float32"),
A: R.Tensor((128, 128), "float32"),
B: R.Tensor((128, 128), "float32"),
C: R.Tensor((127, 1), "float32"),
) -> R.Tensor((127, 128), "float32"):
lv0 = R.matmul(x, A)
Y = R.nn.gelu(lv0)
Z = R.matmul(Y, B)
O = R.nn.mul(Z, C)
return O
AnnotateShardingPass
This pass is for users to describes their sharding strategy through DistIR ‘annotate_sharding’ op.
@I.ir_module
class LoweringDistIRExampleModule:
##### Distributed Environment Infos Begin #####
I.module_attrs({"device_num": 2})
I.module_global_infos({"mesh": [R.device_mesh((2,), I.Range(0, 2))]})
##### Distributed Environment Infos End #####
@R.function
def foo(
x: R.Tensor((128, 128), "float32"),
A: R.Tensor((128, 127), "float32"),
B: R.Tensor((127, 128), "float32"),
C: R.Tensor((128, 1), "float32"),
) -> R.Tensor((128, 128), "float32"):
##### Sharding Strategy Begin #####
A = R.dist.annotate_sharding(A, device_mesh="mesh[0]", placement="S[1]")
##### Sharding Strategy End #####
lv0 = R.matmul(x, A)
Y = R.nn.gelu(lv0)
Z = R.matmul(Y, B)
O = R.multiply(Z, C)
return O
PropagateShardingPass
This pass is provided by DistIR to propagete sharding strategy to the entrie graph.
@I.ir_module
class LoweringDistIRExampleModule:
I.module_attrs({"device_num": 2})
I.module_global_infos({"mesh": [R.device_mesh((2,), I.Range(0, 2))]})
# Represents sharding stategy with DTensor and remove 'annotate_sharding' op.
@R.function
def foo(
x: R.DTensor((128, 128), "float32", "mesh[0]", "R"),
A: R.DTensor((128, 127), "float32", "mesh[0]", "S[1]"),
B: R.DTensor((127, 128), "float32", "mesh[0]", "S[0]"),
C: R.DTensor((128, 1), "float32", "mesh[0]", "R"),
) -> R.DTensor((128, 128), "float32", "mesh[0]", "R"):
A_1: R.DTensor((128, 127), "float32", "mesh[0]", "S[1]") = A
lv0: R.DTensor((128, 127), "float32", "mesh[0]", "S[1]") = R.matmul(x, A_1, out_dtype="void")
Y: R.DTensor((128, 127), "float32", "mesh[0]", "S[1]") = R.nn.gelu(lv0)
Z: R.DTensor((128, 128), "float32", "mesh[0]", "R") = R.matmul(Y, B, out_dtype="void")
O: R.DTensor((128, 128), "float32", "mesh[0]", "R") = R.multiply(Z, C)
return Z
LegalizeShardingPass
In this pass, we use the introduced sharding type ‘I’ to explicitly express reduction semantics that is hided before. This laies down the foundation to employ more optimization in a simple and natrual way.
@I.ir_module
class LoweringDistIRExampleModule:
I.module_attrs({"device_num": 2})
I.module_global_infos({"mesh": [R.device_mesh((2,), I.Range(0, 2))]})
@R.function
def foo(
x: R.DTensor((128, 128), "float32", "mesh[0]", "R"),
A: R.DTensor((128, 127), "float32", "mesh[0]", "S[1]"),
B: R.DTensor((127, 128), "float32", "mesh[0]", "S[0]"),
C: R.DTensor((128, 1), "float32", "mesh[0]", "R"),
) -> R.DTensor((128, 128), "float32", "mesh[0]", "R"):
A_1: R.DTensor((128, 127), "float32", "mesh[0]", "S[1]") = A
lv0: R.DTensor((128, 127), "float32", "mesh[0]", "S[1]") = R.matmul(x, A_1, out_dtype="void")
Y: R.DTensor((128, 127), "float32", "mesh[0]", "S[1]") = R.nn.gelu(lv0)
##### Matmul After Legalization Begin #####
Z_1: R.DTensor((128, 128), "float32", "mesh[0]", "I_sum") = R.matmul(Y, B, out_dtype="void")
Z: R.DTensor((128, 128), "float32", "mesh[0]", "R") = R.dist.redistribute(Z_1, device_mesh="mesh[0]", placement="R")
##### Matmul After Legalization End #####
O: R.DTensor((128, 128), "float32", "mesh[0]", "R") = R.multiply(Z, C)
return O
PreMtrlOptPass
This pass represents a series of global optimizations that should be applied on global unified DistIR. Indeed, it could be multiple passes that run on unified DistIR. Here, we change the order of ‘redistribute’ and ‘multiply’ as an example. After the switch, ‘multiply’ can be fused with ‘matmul’.
@I.ir_module
class LoweringDistIRExampleModule:
I.module_attrs({"device_num": 2})
I.module_global_infos({"mesh": [R.device_mesh((2,), I.Range(0, 2))]})
@R.function
def foo(
x: R.DTensor((128, 128), "float32", "mesh[0]", "R"),
A: R.DTensor((128, 127), "float32", "mesh[0]", "S[1]"),
B: R.DTensor((127, 128), "float32", "mesh[0]", "S[0]"),
C: R.DTensor((128, 1), "float32", "mesh[0]", "R"),
) -> R.DTensor((128, 128), "float32", "mesh[0]", "R"):
A_1: R.DTensor((128, 127), "float32", "mesh[0]", "S[1]") = A
lv0: R.DTensor((128, 127), "float32", "mesh[0]", "S[1]") = R.matmul(x, A_1, out_dtype="void")
Y: R.DTensor((128, 127), "float32", "mesh[0]", "S[1]") = R.nn.gelu(lv0)
Z_1: R.DTensor((128, 128), "float32", "mesh[0]", "I_sum") = R.matmul(Y, B, out_dtype="void")
##### Switch multiply and redistribute Begin #####
Z_2: R.DTensor((128, 128), "float32", "mesh[0]", "R") = R.multiply(Z_1, C)
O: R.DTensor((128, 128), "float32", "mesh[0]", "R") = R.dist.redistribute(Z_2, device_mesh="mesh[0]", placement="R")
##### Switch multiply and redistribute End #####
return O
MaterializeShardingPass
This pass lower the global unified DistIR to ranked single-device Relax IR. This is done by 3 steps:
- First, copy the original IR for each rank
- Second, convert DTensor to Tensor and lower ‘redistribute’ op to actual communication op such as ‘allreduce’. This could be done by visit function signature first, convert its DTensor to Tensor, then propagate the converted Tensor through entire graph.
- Finally, run an elimination pass to eliminate redundant ranked IRs, leaving only one IR for each unique rank.
@I.ir_module
class LoweringDistIRExampleModule:
I.module_attrs({"device_num": 2})
I.module_global_infos({"mesh": [R.device_mesh((2,), I.Range(0, 2))]})
# Ranked Relax IR for rank 0
@R.function
def foo_0(
x: R.Tensor((128, 128), "float32"),
A: R.Tensor((128, 64), "float32"),
B: R.Tensor((64, 128), "float32"),
C: R.Tensor((128, 1), "float32"),
) -> R.Tensor((128, 128), "float32"):
lv0: R.Tensor((128, 64), "float32") = R.matmul(x, A, out_dtype="void")
Y: R.Tensor((128, 64), "float32") = R.nn.gelu(lv0)
Z: R.Tensor((128, 128), "float32") = R.matmul(Y, B_1, out_dtype="void")
Z_1: R.Tensor((128, 128), "float32") = R.multiply(Z, C)
O: R.Tensor((128, 128), "float32") = R.call_packed("vm.dist.allreduce", Z_1, Z_1)
return O
# Rank Relax IR for rank 1
@R.function
def foo_1(
x: R.Tensor((128, 128), "float32"),
A: R.Tensor((128, 63), "float32"),
B: R.Tensor((63, 128), "float32"),
C: R.Tensor((128, 1), "float32"),
) -> R.Tensor((128, 128), "float32"):
##### Padding only happen at rank 1 #####
A_1: R.Tensor((128, 64), "float32") = R.pad(A, (128, 64), value=0)
B_1: R.Tensor((64, 128), "float32") = R.pad(B, (64, 128), value=0)
##### Padding only happen at rank 1 #####
lv0: R.Tensor((128, 64), "float32") = R.matmul(x, A_1, out_dtype="void")
Y: R.Tensor((128, 64), "float32") = R.nn.gelu(lv0)
Z: R.Tensor((128, 128), "float32") = R.matmul(Y, B_1, out_dtype="void")
Z_1: R.Tensor((128, 128), "float32") = R.multiply(Z, C)
O: R.Tensor((128, 128), "float32") = R.call_packed("vm.dist.allreduce", Z_1, Z_1)
return O
PostMtrlOptPass
This pass represents a series of local optimizations that should be applied on ranked single-device Relax IR. Indeed, it could be multiple passes. Here, we fuse ‘multiply’ and ‘matmul’ as an example.
@I.ir_module
class LoweringDistIRExampleModule:
I.module_attrs({"device_num": 2})
I.module_global_infos({"mesh": [R.device_mesh((2,), I.Range(0, 2))]})
# Ranked Relax IR for rank 0
@R.function
def foo_0(
x: R.Tensor((128, 128), "float32"),
A: R.Tensor((128, 64), "float32"),
B: R.Tensor((64, 128), "float32"),
C: R.Tensor((128, 1), "float32"),
) -> R.Tensor((128, 128), "float32"):
lv0: R.Tensor((128, 64), "float32") = R.matmul(x, A, out_dtype="void")
Y: R.Tensor((128, 64), "float32") = R.nn.gelu(lv0)
Z: R.Tensor((128, 128), "float32") = R.fused_matmul_multiply(Y, B_1, C, out_dtype="void")
O: R.Tensor((128, 128), "float32") = R.call_packed("vm.dist.allreduce", Z, Z)
return O
# Rank Relax IR for rank 1
@R.function
def foo_1(
x: R.Tensor((128, 128), "float32"),
A: R.Tensor((128, 63), "float32"),
B: R.Tensor((63, 128), "float32"),
C: R.Tensor((128, 1), "float32"),
) -> R.Tensor((128, 128), "float32"):
##### Padding only happen at rank 1 #####
A_1: R.Tensor((128, 64), "float32") = R.pad(A, (128, 64), value=0)
B_1: R.Tensor((64, 128), "float32") = R.pad(B, (64, 128), value=0)
##### Padding only happen at rank 1 #####
lv0: R.Tensor((128, 64), "float32") = R.matmul(x, A_1, out_dtype="void")
Y: R.Tensor((128, 64), "float32") = R.nn.gelu(lv0)
Z: R.Tensor((128, 128), "float32") = R.fused_matmul_multiply(Y, B_1, C, out_dtype="void")
O: R.Tensor((128, 128), "float32") = R.call_packed("vm.dist.allreduce", Z, Z)
return O
Advantages of the design
In this part, we demonstrate the advantages of the design through example outputs.
Example 1 —— Tail Block
With the following code snippet, we can see that tail block is resolve natrually because we are able to use different IR for each rank. There’re other advantages:
- Enable more ways to tackle irregularities. To resolve tail block, with MPMD we can either padding it or compile a standalone executable(but most kernel executables can be shared) for that particular rank. We can also fallback to SPMD since it is just a special case of MPMD.
- No need to invent new infrastructure. With MPMD, we resolve irregularities at the expense of redundancy, this enables us to reuse all infrastructure TVM provides now, including operator inventory, optimization passes, lowering passes and etc. Since each ranked IR is just a single-device IR which TVM
- Enables more optimization oppourtunities. In the example below, tensor B on rank 1 has a shape of (128, 2), applying padding on it wastes extra memory. With MPMD, we can compile kernels specifically for its shape and save those memory.
@I.ir_module
class TailBlockExample:
I.module_attrs({"device_num": 2})
I.module_global_infos({"mesh": [R.device_mesh((2,), I.Range(0, 2))]})
# Ranked Relax IR for rank 0
@R.function
def foo_0(
x: R.Tensor((128, 128), "float32"),
A: R.Tensor((128, 64), "float32"),
B: R.Tensor((64, 128), "float32"),
C: R.Tensor((128, 1), "float32"),
) -> R.Tensor((128, 128), "float32"):
lv0: R.Tensor((128, 64), "float32") = R.matmul(x, A, out_dtype="void")
Y: R.Tensor((128, 64), "float32") = R.nn.gelu(lv0)
Z: R.Tensor((128, 128), "float32") = R.matmul(Y, B_1, out_dtype="void")
Z_1: R.Tensor((128, 128), "float32") = R.call_packed("vm.dist.allreduce", Z, Z)
O: R.Tensor((128, 128), "float32") = R.multiply(Z_1, C)
return O
# Rankde Relax IR for rank 1
@R.function
def foo_1(
x: R.Tensor((128, 128), "float32"),
A: R.Tensor((128, 2), "float32"),
B: R.Tensor((2, 128), "float32"),
C: R.Tensor((128, 1), "float32"),
) -> R.Tensor((128, 128), "float32"):
##### Padding only happen at rank 1 #####
A_1: R.Tensor((128, 64), "float32") = R.pad(A, (128, 64), value=0)
B_1: R.Tensor((64, 128), "float32") = R.pad(B, (64, 128), value=0)
##### Padding only happen at rank 1 #####
lv0: R.Tensor((128, 64), "float32") = R.matmul(x, A_1, out_dtype="void")
Y: R.Tensor((128, 64), "float32") = R.nn.gelu(lv0)
Z: R.Tensor((128, 128), "float32") = R.matmul(Y, B_1, out_dtype="void")
Z_1: R.Tensor((128, 128), "float32") = R.call_packed("vm.dist.allreduce", Z, Z)
O: R.Tensor((128, 128), "float32") = R.multiply(Z_1, C)
return O
Example 2 —— Sharding CONV Op
With the following code snippet, we can see that sharding along spatial axis of sliding window operators is also resolve natrually. Some other advatnges including:
- No need to invent complex communication operators. With this design, complex communication logics can be expressed by simple ops, e.g. send and recv.
- Enables more general and composable optimizations. Another advantage of using simple communication ops to build more complex communication logics is that optimization patterns and passes need only targets those basic building blocks, enables more general, composable optimizations.
@I.ir_module
class ShardingConvExample:
I.module_attrs({"device_num": 2})
I.module_global_infos({"mesh": [R.device_mesh((2,), I.Range(0, 2))]})
@R.function
def foo_0(
a: R.Tensor((1, 3, 5, 3), "float32"), # N, H, W, Cin
w: R.Tensor((3, 3, 3, 10), "float32") # Kh, Kw, Cin, Cout
) -> R.Tensor((1, 2, 5, 10), "float32"):
# Recive from rank 1
from_rank1 = R.alloc_tensor((1, 1, 5, 3), "float32")
R.call_packed("vm.dist.recv", from_rank1, sendRank=1)
# Send to rank 1
to_rank1 = R.slice(a, begin=[0, 2, 0, 0], end=[1, 3, 5, 3])
R.call_packed("vm.dist.send", to_rank1, recvRank=1)
# Concate local activation
a_0 = R.concate(a, from_rank1, axis=1)
# Execute conv2d
r = R.conv2d(a0, w)
return r
@R.function
def foo_1(
a: R.Tensor((1, 2, 5, 3), "float32"), # N, H, W, Cin
w: R.Tensor((3, 3, 3, 10), "float32") # Kh, Kw, Cin, Cout
) -> R.Tensor((1, 1, 5, 10), "float32"):
# Send to rank 0
to_rank0 = R.slice(a, begin=[0, 0, 0, 0], end=[1, 1, 5, 3])
R.call_packed("vm.dist.send", to_rank0, recvRank=0)
# Recive from rank 0
from_rank0 = R.alloc_tensor((1, 1, 5, 3), "float32")
R.call_packed("vm.dist.recv", from_rank0, sendRank=0)
# Concate local activation
a_1 = R.concate(a, from_rank0, axis=1)
# Execute conv2d
r = R.conv2d(a_1, w)
return r
Example 3 —— Introducing ‘I’ in Sharding Type
Antoher design choice we made is to add a new sharding type ‘I’ which stands for intermediate. From the example below, we can see that by explicitly express intermediate tensor that is waiting to be reduced, we can enables more fusion oppourtunities.
# Without Sharding Type "I"
@I.ir_module
class LoweringDistIRExampleModule:
I.module_attrs({"device_num": 2})
I.module_global_infos({"mesh": [R.device_mesh((2,), I.Range(0, 2))]})
@R.function
def foo(
A: R.DTensor((128, 8), "float32", "mesh[0]", "S[1]"),
B: R.DTensor((128, 128), "float32", "mesh[0]", "S[0]"),
C: R.DTensor((128, 1), "float32", "mesh[0]", "R"),
) -> R.DTensor((128, 128), "float32", "mesh[0]", "R"):
# We cannot fuse 'multiply' into matmul because of the implicit reduce.
# If we want to force the fusion, new patterns or rules that identifies the implicit reduce must be developed.
D_1: R.DTensor((128, 128), "float32", "mesh[0]", "R") = R.matmul(A, B, out_dtype="void")
O: R.DTensor((128, 128), "float32", "mesh[0]", "R") = R.multiply(D, C)
return O
# With Sharding Type "I"
@I.ir_module
class LoweringDistIRExampleModule:
I.module_attrs({"device_num": 2})
I.module_global_infos({"mesh": [R.device_mesh((2,), I.Range(0, 2))]})
@R.function
def foo(
A: R.DTensor((128, 8), "float32", "mesh[0]", "S[1]"),
B: R.DTensor((128, 128), "float32", "mesh[0]", "S[0]"),
C: R.DTensor((128, 1), "float32", "mesh[0]", "R"),
) -> R.DTensor((128, 128), "float32", "mesh[0]", "R"):
D_1: R.DTensor((128, 128), "float32", "mesh[0]", "I_SUM") = R.matmul(A, B, out_dtype="void")
# The order of 'redistribute' and 'multiply' can be switched and then 'multiply' can be fused into 'matmul'
D: R.DTensor((128, 128), "float32", "mesh[0]", "R") = R.dist.redistribute(D_1, device_mesh="mesh[0]", placement="I_SUM")
O: R.DTensor((128, 128), "float32", "mesh[0]", "R") = R.multiply(D, C)
return O
There’re other advantages of the design:
- Enables local optimizations. Split the IR for each unique ranks enables us to optimize each ranked IR separately and locally.
- More layered organization of optimizations and passes. By introducing Ranked Relax IRModule, the optimization and analysis can be naturally separated to two categories, a global one that should be applied on unified DistIR and a local one that should be applied on ranked IR.
Disadvantages of the design
Some disadvantages of this design including:
- Local optimizations on communications are subject to deadlock. Since we split the IR to multiple ranked one, deadlock may happend when we apply local optimizations, such as changing the order of communication ops. This could be solved by introduce a helper ‘barrier’ op, only ops inside the same barrier region can be switched.
- Indroduce extra compilation overhead. For large-scale distributed application, we may need to compile a large number of ranked IR, this brings extra compilation overhead. Also, the size of the executable may inflate.
- Extra runtime complexity. Runtime now need to support MPMD paradigm, requires further engineering effort.
Future Possibilities
Some future directions including:
- Explore ways to combine distributed inference with other LLM optimizations, such as KVCache, paged memory management and continuous batching.
- Exolore possible compiler-level optimizations including optimizations of communication ops and optimization between communication ops and compute ops.
- Explore ways to support asynchronous inference. This could be helpful for pipeline paralliesm to fully utilize device resources and improve throughput.
Our Plan
Since all works in the filed of distributed inference/training are at very early stage, including our design which has not been started to implement, we expect to discuss with community in a broader and deeper way to avoid any possible repeat work and conflicts in designs.
Authors
Kwai AI Platform Compiler Group.