Introduction
Many Deep Learning workloads involve sparse/variable components, e.g. Mixture of Experts, Network Pruning, GNNs, and Sparse Conv. Currently, if users want to write these operators in TVM, they need to compose them with IRBuilder, which is not scalable and cannot be specified schedules.
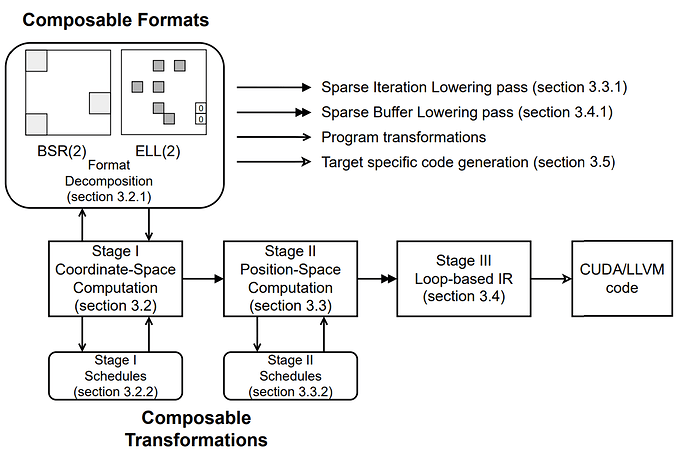
SparseTIR is our attempt at bringing sparsity to TVM, the basic idea is to build a dialect on top of TVM’s TensorIR, and adding sparse annotations (inspired by TACO and other pioneering works in sparse compilers) as first-class members to describe formats for sparse tensors and sparse iterations. SparseTIR designs a multi-stage compilation process whose frontend IR is TACO-like sparse computation description and target IR is TensorIR:
A lot of optimizations and generalizations can be done under this framework. Notably composable formats and composable transformations: we can decompose the computation into several different formats where each one of them in different formats (usually more hardware friendly), and optimize computation on each one of these formats. The multi-stage design enables us to apply schedule primitives in different stages, at both high-level (stage-I) for sparsity-aware transformations and lower-level (stage-II) to reuse TVM’s schedule primitives.
Programming Interface
A generic SparseTIR program looks like the following, the workload is Sampled-Dense-Dense-Matrix-Multiplication (SDDMM):
@T.prim_func
def sddmm(
a: T.handle,
b: T.handle,
x: T.handle,
y: T.handle,
indptr: T.handle,
indices: T.handle,
m: T.int32,
n: T.int32,
feat_size: T.int32,
nnz: T.int32,
) -> None:
T.func_attr({"global_symbol": "main", "tir.noalias": True, "sparse_tir_level": 2})
# sparse axes
I = T.dense_fixed(m)
J = T.sparse_variable(I, (n, nnz), (indptr, indices), "int32")
J_detach = T.dense_fixed(n)
K = T.dense_fixed(feat_size)
# sparse buffers
A = T.match_sparse_buffer(a, (I, K), "float32")
B = T.match_sparse_buffer(b, (J_detach, K), "float32")
X = T.match_sparse_buffer(x, (I, J), "float32")
Y = T.match_sparse_buffer(y, (I, J), "float32")
# sparse iterations
with T.sp_iter([I, J, K], "SSR", "sddmm") as [i, j, k]:
with T.init():
Y[i, j] = 0.0
Y[i, j] = Y[i, j] + A[i, k] * B[j, k] * X[i, j]
where we have constructs like sparse axes, sparse buffers and sparse iterations.
Sparse Axis
Sparse axis is a generation of per-dimensional level formats in TACO where we annotate each dimension of a format as dense/sparse (this dimension is stored in dense or compressed storage) and fixed/variable (this dimension’s extent is fixed or variable). For sparse/variable axes, we need to specify its dependent axis.
- For axes that are sparse, we need to specify a
indicesarray to store the column indices. - For axes that are variable, we need to specify an
indptr(short for indices pointer) array to store the start offset of each row because the row length is variable and we cannot simply compute element offset with an affine map of indices. - An axes that is both sparse and variable need to be specified with both indices and indptr array.
I = T.dense_fixed(m)
# J1 is a sparse fixed axis, whose dependent axis is I
# it has maximum length n and number of non-zero elements per row: c,
# the column indices data are stored in the region started from indices_1 handle,
# and the index data type (in indices array) is int32.
J1 = T.sparse_fixed(I, (n, c), indices_1, idtype="int32")
# J2 is a dense variable axis, whose dependent axis is I,
# it has a maximum length of n,
# the indptr data are stored in the region started from indptr_2 handle,
# and the index data type (in indptr array) is int32.
J2 = T.dense_variable(I, n, indptr_2, idtype="int32")
# J3 is a sparse variable axis, whose dependent axis is J1,
# it has maximum length of n1, number of elements nnz in the space composed of (I, J1, J3),
# the indptr data are stored in the region started from indptr_3 handle,
# and the indices data are stored in the region started from indices_3 handle,
# the index data type (of indptr and indices array) is "int64")
J3 = T.sparse_variable(J1, (n1, nnz), (indptr_3, indices_3), idtype="int34")
Sparse Buffer
User can create sparse buffers with following APIs in SparseTIR:
A = T.match_sparse_buffer(a, (I, J1), dtype="float32", scope="global")
B = T.alloc_sparse_buffer((I, j2), dtype="float32", scope="shared")
Their semantics are very similar to the existing match_buffer and alloc_buffer constructs in TensorIR, with the exception that we accept an array of sparse axes as shape.
- The
match_sparse_bufferbinds a sparse format with a handle(pointer)ato the start of a user-specified input/output array that stores the value inside the sparse buffer. - The
alloc_sparse_buffercreate a sparse buffer without binding to input or output and always acts as an intermediate buffer.
The storage of sparse tensors in SparseTIR follows the design of Compressed Sparse Fiber which is a natural extension of CSR format to high dimensional. Note that SparseTIR decouples the storage of value with auxiliary structure information such as indptr and indices: the value array is bonded with sparse buffers and the indptr and indices array is bonded to axes. Such design enables us to share structure information for different buffers (e.g. in the SDDMM example shown above, the X and Y sparse buffers share structure and we don’t need duplicate storage for their indptr and indices).
We can express sparse tensors stored in various formats using the sparse axis and sparse buffer construct:
# ELLPack format, with number of columns per row 4
I = T.dense_fixed(m)
J = T.sparse_fixed(I, (n, 4), indices, idtype="int32")
A = T.match_sparse_buffer(a, (I, J), dtype="float32")
# 2D Ragged Tensor
I = T.dense_fixed(m)
J = T.dense_variable(I, n, indptr, idtype="int32")
A = T.match_sparse_buffer(a, (I, J), dtype="float32")
# Doubly Compressed Sparse Row (DCSR)
O = T.dense_fixed(1) # A placeholder axis to create axis I.
I = T.sparse_variable(O, (m, nnz1), (indptr_i, indices_i), idtype="int32")
J = T.sparse_variable(I, (n, nnz2), (indptr_j, indices_j), idtype="int32")
A = T.match_sparse_buffer(a, (O, I, J), dtype="float32")
# Block Compressed Sparse Row (BCSR)
IO = T.dense_fixed(mb)
JO = T.sparse_variable(IO, (nb, nnzb), (indptr, indices), idtype="int32")
II = T.dense_fixed(block_size)
JI = T.dense_fixed(block_size)
A = T.match_sparse_buffer(a, (IO, JO, II, JI), dtype="float32")
Sparse Iteration
To create an iteration space, SparseTIR provides a structure called sparse iteration, which accepts an array of sparse axes as input and emits correspondingly iterators on these axes, user can write computations inside the body of sparse iterations:
with T.sp_iter([I, J, K], "SSR", "sddmm") as [i, j, k]:
with T.init():
Y[i, j] = 0.0
Y[i, j] = Y[i, j] + A[i, k] * B[j, k] * X[i, j]
here the SSR means the three iterators are spatial or reduction, which follows the design of TensorIR. sddmm is the name of the sparse iteration for reference when applying schedule primitives.
Compiler Passes
SparseTIR has three major compiler passes: DecomposeFormat, LowerSparseIter and LowerSparseBuffer.
(Optional) Decompose Format
As mentioned above, SparseTIR supports composable formats for efficiency on heterogeneous hardware, this is achieved by an optional compiler pass called DecomposeFormat.
We provide a class called FormatRewriteRule which is a specification of a format rewrite rule, and the pass would accept an array of FormatRewriteRules and rewrites the given SparseTIR script by :
# original sparsetir script before rewrite
@T.prim_func
def csrmm(
a: T.handle,
b: T.handle,
c: T.handle,
indptr: T.handle,
indices: T.handle,
m: T.int32,
n: T.int32,
feat_size: T.int32,
nnz: T.int32,
) -> None:
T.func_attr({"global_symbol": "main", "tir.noalias": True, "sparse_tir_level": 2})
I = T.dense_fixed(m)
J = T.sparse_variable(I, (n, nnz), (indptr, indices), "int32")
J_detach = T.dense_fixed(n)
K = T.dense_fixed(feat_size)
A = T.match_sparse_buffer(a, (I, J), "float32")
B = T.match_sparse_buffer(b, (J_detach, K), "float32")
C = T.match_sparse_buffer(c, (I, K), "float32")
with T.sp_iter([I, J, K], "SRS", "csrmm") as [i, j, k]:
with T.init():
C[i, k] = 0.0
C[i, k] = C[i, k] + A[i, j] * B[j, k]
mod = tvm.IRModule.from_expr(csrmm)
# bsr format description
def bsr(block_size: int):
@T.prim_func
def func(
a: T.handle,
indptr: T.handle,
indices: T.handle,
m: T.int32,
n: T.int32,
nnz: T.int32
) -> None:
IO = T.dense_fixed(m)
JO = T.sparse_variable(IO, (n, nnz), (indptr, indices), "int32")
II = T.dense_fixed(block_size)
JI = T.dense_fixed(block_size)
A = T.match_sparse_buffer(a, (IO, JO, II, JI), "float32")
T.evaluate(0) # placeholder, indicates it's the end of the script.
return func
# inverse index map
def csr2bsr_inv_index_map(block_size):
def func(io, jo, ii, ji):
return io * block_size + ii, jo * block_size + ji
return func
# index map
def csr2bsr_index_map(block_size):
def func(i, j):
return i // block_size, j // block_size, i % block_size, j % block_size
return func
block_size_symbol = bsr.params[-1]
rewrites = [] # array of format rewrite rules
for block_size in [4, 16, 32]:
rewrites.append(
FormatRewriteRule(
str(block_size), # name of generated buffer.
bsr.specialize({block_size_symbol: block_size}), # the format specification
["A"], # name of the original buffer to rewrite
["I", "J"], # names of the axes the constructs the original buffer
["IO", "JO", "II", "JI"], # names of the axis that constructs new buffer
{"I": ["IO", "II"], "J": ["JO", "JI"]}, # the correspondence between original axes and new axes
csr2bsr_index_map(block_size), # the index map from the original buffer access index to the new
buffer access index.
csr2bsr_inv_index_map(block_size), # the inverse index map from new buffer access index to original buffer access index.
)
)
# format decomposition pass
mod = tvm.sparse.format_decompose(mod, rewrites)
and below is the IR script after transformation, which generates three 3 sparse iterations for data movement that copies data from the original format to composable formats, and another 3 sparse iterations that compute on the composable formats:
@T.prim_func
def bsr_rewrite_with_preprocess(
a: T.handle,
b: T.handle,
c: T.handle,
indptr: T.handle,
indices: T.handle,
m: T.int32,
n: T.int32,
feat_size: T.int32,
nnz: T.int32,
a_4: T.handle,
indptr_4: T.handle,
indices_4: T.handle,
m_4: T.int32,
n_4: T.int32,
nnz_4: T.int32,
a_16: T.handle,
indptr_16: T.handle,
indices_16: T.handle,
m_16: T.int32,
n_16: T.int32,
nnz_16: T.int32,
a_32: T.handle,
indptr_32: T.handle,
indices_32: T.handle,
m_32: T.int32,
n_32: T.int32,
nnz_32: T.int32,
) -> None:
# function attr dict
T.func_attr(
{"global_symbol": "main", "tir.noalias": True, "sparse_tir_level": 2, "composable": 1}
)
I = T.dense_fixed(m, "int32")
J = T.sparse_variable(I, (n, nnz), (indptr, indices), "int32")
J_detach = T.dense_fixed(n, "int32")
K = T.dense_fixed(feat_size, "int32")
IO_4 = T.dense_fixed(m_4, "int32")
JO_4 = T.sparse_variable(IO_4, (n_4, nnz_4), (indptr_4, indices_4), "int32")
II_4 = T.dense_fixed(4, "int32")
JI_4 = T.dense_fixed(4, "int32")
IO_16 = T.dense_fixed(m_16, "int32")
JO_16 = T.sparse_variable(IO_16, (n_16, nnz_16), (indptr_16, indices_16), "int32")
II_16 = T.dense_fixed(16, "int32")
JI_16 = T.dense_fixed(16, "int32")
IO_32 = T.dense_fixed(m_32, "int32")
JO_32 = T.sparse_variable(IO_32, (n_32, nnz_32), (indptr_32, indices_32), "int32")
II_32 = T.dense_fixed(32, "int32")
JI_32 = T.dense_fixed(32, "int32")
A = T.match_sparse_buffer(a, [I, J], dtype="float32")
B = T.match_sparse_buffer(b, [J_detach, K], dtype="float32")
C = T.match_sparse_buffer(c, [I, K], dtype="float32")
A_4 = T.match_sparse_buffer(a_4, [IO_4, JO_4, II_4, JI_4], dtype="float32")
A_16 = T.match_sparse_buffer(a_16, [IO_16, JO_16, II_16, JI_16], dtype="float32")
A_32 = T.match_sparse_buffer(a_32, [IO_32, JO_32, II_32, JI_32], dtype="float32")
# body
# with T.block("root")
with T.sp_iter([IO_4, JO_4, II_4, JI_4], "SSSS", "rewrite_A_4") as [io_4, jo_4, ii_4, ji_4]:
T.sp_iter_attr({"preprocess": True})
A_4[io_4, jo_4, ii_4, ji_4] = A[io_4 * 4 + ii_4, jo_4 * 4 + ji_4]
with T.sp_iter([IO_16, JO_16, II_16, JI_16], "SSSS", "rewrite_A_16") as [
io_16,
jo_16,
ii_16,
ji_16,
]:
T.sp_iter_attr({"preprocess": True})
A_16[io_16, jo_16, ii_16, ji_16] = A[io_16 * 16 + ii_16, jo_16 * 16 + ji_16]
with T.sp_iter([IO_32, JO_32, II_32, JI_32], "SSSS", "rewrite_A_32") as [
io_32,
jo_32,
ii_32,
ji_32,
]:
T.sp_iter_attr({"preprocess": True})
A_32[io_32, jo_32, ii_32, ji_32] = A[io_32 * 32 + ii_32, jo_32 * 32 + ji_32]
with T.sp_iter([IO_4, II_4, JO_4, JI_4, K], "SSRRS", "csrmm_4") as [io_4, ii_4, jo_4, ji_4, k]:
with T.init():
C[io_4 * 4 + ii_4, k] = T.float32(0)
C[io_4 * 4 + ii_4, k] = (
C[io_4 * 4 + ii_4, k] + A_4[io_4, jo_4, ii_4, ji_4] * B[jo_4 * 4 + ji_4, k]
)
with T.sp_iter([IO_16, II_16, JO_16, JI_16, K], "SSRRS", "csrmm_16") as [
io_16,
ii_16,
jo_16,
ji_16,
k,
]:
with T.init():
C[io_16 * 16 + ii_16, k] = T.float32(0)
C[io_16 * 16 + ii_16, k] = (
C[io_16 * 16 + ii_16, k] + A_16[io_16, jo_16, ii_16, ji_16] * B[jo_16 * 16 + ji_16, k]
)
with T.sp_iter([IO_32, II_32, JO_32, JI_32, K], "SSRRS", "csrmm_32") as [
io_32,
ii_32,
jo_32,
ji_32,
k,
]:
with T.init():
C[io_32 * 32 + ii_32, k] = T.float32(0)
C[io_32 * 32 + ii_32, k] = (
C[io_32 * 32 + ii_32, k] + A_32[io_32, jo_32, ii_32, ji_32] * B[jo_32 * 32 + ji_32, k]
)
This pass can help generate code with better performance if we use the “right” composable formats. However, it introduces external data movement overhead from the buffer in the original format to the buffer in composable formats. In most settings where the sparse structure is stationary, we can lift the data movement parts outside the kernel and reuse them during training/serving thus amortizing such overhead. But there are some cases that sparse structure is dynamic and decompose format is not necessary, so we make this pass optional.
Sparse Iteration Lowering
The transition from stage-I to stage-II is called Sparse Iteration Lowering where we restructure Sparse Iterations in stage-I to nested loops in stage-II (in the future we will support co-iterations generation like in TACO), and we also change the buffer access semantics from coordinate space in stage-I (which is data structure agnostic) to position space in stage-II (which is aware of data structures).
Below is an example of sparse iteration lowering:
# before lowering
@T.prim_func
def bsrmm_stage_i(
a: T.handle,
b: T.handle,
c: T.handle,
indptr: T.handle,
indices: T.handle,
nb: T.int32,
mb: T.int32,
nnzb: T.int32,
blk: T.int32,
feat_size: T.int32,
) -> None:
T.func_attr({"global_symbol": "main", "tir.noalias": True, "sparse_tir_level": 2})
I = T.dense_fixed(nb)
J = T.sparse_variable(I, (mb, nnzb), (indptr, indices), "int32")
J_detach = T.dense_fixed(mb)
BI = T.dense_fixed(blk)
BJ = T.dense_fixed(blk)
F = T.dense_fixed(feat_size)
A = T.match_sparse_buffer(a, (I, J, BI, BJ), "float32")
B = T.match_sparse_buffer(b, (J_detach, BJ, F), "float32")
C = T.match_sparse_buffer(c, (I, BI, F), "float32")
with T.sp_iter([I, BI, BJ, F, J], "SSRSR", "bsrmm") as [
i,
bi,
bj,
f,
j,
]:
with T.init():
C[i, bi, f] = 0.0
C[i, bi, f] = C[i, bi, f] + A[i, j, bi, bj] * B[j, bj, f]
# after lowering
@T.prim_func
def bsrmm_stage_ii(
a: T.handle,
b: T.handle,
c: T.handle,
indptr: T.handle,
indices: T.handle,
nb: T.int32,
mb: T.int32,
nnzb: T.int32,
blk: T.int32,
feat_size: T.int32,
) -> None:
# function attr dict
T.func_attr({"global_symbol": "main", "tir.noalias": True, "sparse_tir_level": 1})
I = T.dense_fixed(nb, idtype="int32")
J = T.sparse_variable(I, (mb, nnzb), (indptr, indices), idtype="int32", sorted=True)
J_dense = T.dense_variable(I, (mb, nnzb), indptr, idtype="int32")
J_detach = T.dense_fixed(mb, idtype="int32")
BI = T.dense_fixed(blk, idtype="int32")
BJ = T.dense_fixed(blk, idtype="int32")
F = T.dense_fixed(feat_size, idtype="int32")
A = T.match_sparse_buffer(a, [I, J, BI, BJ], dtype="float32")
B = T.match_sparse_buffer(b, [J_detach, BJ, F], dtype="float32")
C = T.match_sparse_buffer(c, [I, BI, F], dtype="float32")
J_indptr = T.match_sparse_buffer(indptr, [I], dtype="int32", extra_storage=1)
J_indices = T.match_sparse_buffer(indices, [I, J_dense], dtype="int32")
# body
# with T.block("root")
T.assume_buffer_domain(J_indptr, [0, nnzb])
T.assume_buffer_domain(J_indices, [0, mb])
for i, bi, bj, f in T.grid(nb, blk, blk, feat_size):
with T.block("bsrmm0"):
vi, vbi, vbj, vf = T.axis.remap("SSRS", [i, bi, bj, f])
T.reads(
J_indptr[vi : vi + 2], A[vi, 0:mb, vbi, vbj], B[0:mb, vbj, vf], J_indices[vi, 0:mb]
)
T.writes(C[vi, vbi, vf])
T.block_attr({"sparse": True})
with T.init():
C[vi, vbi, vf] = T.float32(0)
for j in T.serial(J_indptr[vi + 1] - J_indptr[vi]):
with T.block("bsrmm1"):
vj = T.axis.reduce(mb, j)
T.reads(A[vi, vj, vbi, vbj], B[J_indices[vi, vj], vbj, vf], J_indices[vi, vj])
T.writes(C[vi, vbi, vf])
T.block_attr({"sparse": True})
C[vi, vbi, vf] = (
C[vi, vbi, vf] + A[vi, vj, vbi, vbj] * B[J_indices[vi, vj], vbj, vf]
)
Please check section 3.3 of the paper and code for the details of this pass.
Sparse Buffer Lowering
This pass transforms stage-II IR to stage-III IR (TVM TensorIR), by removing sparse structures (axes and sparse buffers), and flattens sparse buffer access to underlying 1-dimensional compressed storage access.
Below is the code of BSRMM function in stage-III after sparse buffer lowering:
@T.prim_func
def bsrmm(
a: T.handle,
b: T.handle,
c: T.handle,
indptr: T.handle,
indices: T.handle,
nb: T.int32,
mb: T.int32,
nnzb: T.int32,
blk: T.int32,
feat_size: T.int32,
) -> None:
# function attr dict
T.func_attr({"global_symbol": "main", "tir.noalias": True, "sparse_tir_level": 0})
A_data = T.match_buffer(a, [nnzb * blk * blk], dtype="float32", strides=[1])
B_data = T.match_buffer(b, [mb * blk * feat_size], dtype="float32", strides=[1])
C_data = T.match_buffer(c, [nb * blk * feat_size], dtype="float32", strides=[1])
J_indptr_data = T.match_buffer(indptr, [nb + 1], dtype="int32", strides=[1])
J_indices_data = T.match_buffer(indices, [nnzb], dtype="int32", strides=[1])
# body
# with T.block("root")
for i, bi, bj, f in T.grid(nb, blk, blk, feat_size):
with T.block("bsrmm0"):
vi, vbi, vbj, vf = T.axis.remap("SSRS", [i, bi, bj, f])
T.reads(
J_indptr_data[0 : nb + 1],
A_data[0 : nnzb * blk * blk],
B_data[0 : mb * blk * feat_size],
J_indices_data[0:nnzb],
)
T.writes(C_data[vi * (blk * feat_size) + vbi * feat_size + vf])
T.block_attr({"sparse": True})
with T.init():
C_data[vi * (blk * feat_size) + vbi * feat_size + vf] = T.float32(0)
for j in T.serial(J_indptr_data[vi + 1] - J_indptr_data[vi]):
with T.block("bsrmm1"):
vj = T.axis.reduce(mb, j)
T.reads(
A_data[(vj + J_indptr_data[vi]) * (blk * blk) + vbi * blk + vbj],
B_data[
J_indices_data[vj + J_indptr_data[vi]] * (blk * feat_size)
+ vbj * feat_size
+ vf
],
J_indices_data[vj + J_indptr_data[vi]],
)
T.writes(C_data[vi * (blk * feat_size) + vbi * feat_size + vf])
T.block_attr({"sparse": True})
C_data[vi * (blk * feat_size) + vbi * feat_size + vf] = (
C_data[vi * (blk * feat_size) + vbi * feat_size + vf]
+ A_data[(vj + J_indptr_data[vi]) * (blk * blk) + vbi * blk + vbj]
* B_data[
J_indices_data[vj + J_indptr_data[vi]] * (blk * feat_size)
+ vbj * feat_size
+ vf
]
)
Please refer to section 3.4 in the paper and code for details of this pass.
Schedules and Post-Processing Passes
We allow users to apply schedule primitives at all stages (I, II, III) to transform programs.
Stage-I Schedules
The schedules applied at stage-I are new to TVM, we require schedule primitives at this stage to only manipulates the 3 structures Axes, Sparse Iterations, and Sparse Buffers, and cannot generate loops/blocks because these structures do not appear in stage-I. We currently have the following schedules at stage-I:
- sparse_reorder : reorder the iterators in sparse iterations.
- sparse_fuse : fuse multiple iterators into a single one, so that we only emit a single loop for the multi-dimensional iteration space in stage-II (this is the same as
collapseschedule primitive in TACO). - annotate_sparse_iter : annotate sparse iterations.
We can create more schedule primitives such as sparse_compute_at as long as they are dealing with stage-I structures.
Stage-II/III Schedules
Stage-I is very similar to TensorIR except for Axes and Sparse Buffers, we re-use all TensorIR’s schedule primitives to enable transforming stage-II/III IR in SparseTIR.
Slight code changes are required to make some schedule primitives recognize sparse buffers, but in general, these changes would not break any existing behavior.
Post-Processing Passes
Horizontal Fusion
We need a HorizontalFusion pass which enables us to fuse multiple CUDA kernels horizontally (to reduce kernel launching overhead for composable formats, on CUDA):
The pass itself is not hard to implement in TVM, reference implementation can be found here.
Lowering Atomic Intrinsics
Several CTA might write into the same position because of composable formats, and this pass would rewrite assignments to atomic add (and more general atomic aggregation, in the future) intrinsics.
Runtime classes
The Decompose Format pass is only responsible for rewriting the IR, and we need corresponding functions to transform the sparse matrix, currently, SparseTIR is not capable of generating these format conversion routines automatically, but we provide APIs for some frequently used conversions.
How can SparseTIR benefit the TVM project
SparseTIR can help TVM support sparse workloads in Deep Learning, currently, TVM has some sparse workloads written in IRBuilder and we can replace them with SparseTIR scripts, which also enables larger schedule space as IRBuilder is hard to schedule. We have evaluated many sparse Deep Learning applications in SparseTIR and the performance is promising (see our examples and artifact evaluations).
SparseTIR’s design is consistent with the spirit of TVM Unity, the sparse annotations could not only exist in tensor level IR but also computational-graph level IR (e.g. relax), where we can describe variable lengths inputs in LLMs, mixture-of-experts and more.
Changes to the TVM codebase
Thanks to the modular design of TVMScript, the changes to the TVM codebase are minimal and incremental, and we can ship these features one by one:
- Sparse Data Structures
- SparseTIR TVMScript parser and printer and unit tests
- SparseTIR schedule primitives and unit tests
- Lowering passes and unit tests
- Decompose Formats
- Sparse Iteration Lowering
- Sparse Buffer Lowering
- Horizontal Fusion
- Atomic Lowering
- …
- Runtime classes and unit tests
We haven’t designed the proper algorithm for auto-scheduling SparseTIR, but it will be interesting to see MetaSchedule (or a faster default scheduler) for SparseTIR.
Some items to discuss
- Should we reuse the
Tprefix for SparseTIR structures, or create a new name space such asSbecause sparse annotations can be used in different level IRs (e.g. TensorIR and Relax). - We change the
PrimFuncnode to add a fieldsparse_axeswhich is an array of Axes, its default value is empty. This would change the initialization function ofPrimFunc, I’m not sure if it’s acceptable for the community. An alternative is to create a subclassSparsePrimFuncand not change the behavior of existingPrimFunc.
References
- SparseTIR paper
- SparseTIR repository
- SparseTIR artifacts
- Stage-I scripts
- Stage-II scripts
- Stage-III scripts
Authors: The SparseTIR Team(@yzh119 @MasterJH5574 @junrushao @tqchen ).
We look forward to hearing more feedback from the community.