Search-based Automated Quantization
Background
One year before, I have implemented a quantization workflow in tvm: issue, pull. Brought the idea from some existing quantization frameworks, I choose to adopt the annotation-calibration-realization 3-phases design:
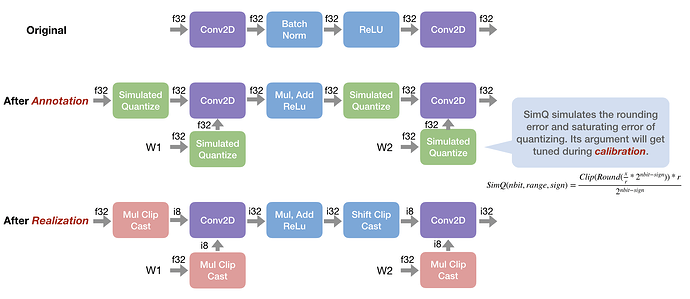
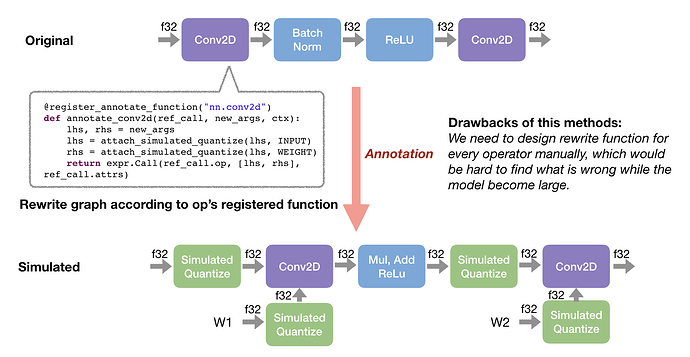
- Annotation: The annotation pass rewrites the graph and inserts simulated quantize operation according to the rewrite function of each operator. The simulated quantize operation simulates the rounding error and saturating error of quantizing from float to integer,
- Calibration: The calibration pass will adjust thresholds of simulated quantize operations to reduce the accuracy dropping.
- Realization: The realization pass transforms the simulation graph, which computes with float32 actually, to a real low-precision integer graph.
However, during development, I found there exist some drawbacks in this approach:
- During annotation, we annotate each tensor as
INPUT/WEIGHT/ACTIVATIONkind for different quantization stratege, which is kinds of operation specific, so that we need to hanle different combinations happened in different models. This make annotation has many manual rules and becomes quite hard to maintain. See here as example. - The simulated graph don’t have the total scale and data type information. We defer the scale inference and data type selection to realization, which makes logic of this part quite hard to understand. Also, lacking of those information means that we cannot catch overflow error during simulation.
- We are facing hardware divergence while trying to deploy quantized model to different hardwares. There are two solutions: 1.checking target during annotation, which make the logic more complicated; 2.adding a new partition pass to decide the quantize topology first, which means every hardware need to implement a customized partition pass.
Based on the previous experience we have learnt, I am proposing a new quantization framework, which brings hardware and learning method in the loop. Serveral improvements have been made to address our previous problems:
- Inserting SimQ (simulated_quantize) operation on every edge instead of by manual annotation rule. Let the learning algorithm to discover the best quantization strategy on every edge instead of by labeling.
- Adding
in_scale,in_dtype,out_dtypeinto SimQ’s definition. Executing scale inference and data type assignment during simulation. Simulating overflow error in SimQ. - Proposing the
Hardwareabstraction to describe hardware properties and operation constraints. By this declaration way, users only need to define differentHardwareobjects for different hardwares, without need to understand the quantization logic.
Workflow Overview
Let’s walk through the workflow first.
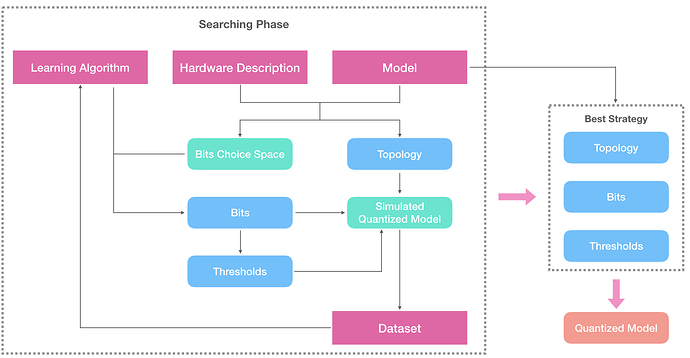
GIven the model and a description for the target hardware, the system will generate a set of choice space for bits, and the Topology of the quantization. Here Topology means which nodes / edges will be quantized, considering the hardware and operator contraints, which will be discussed later.
Then the search loop begins: the learning algorithm will select a set of parameter from the choice space – here is the number of bit on every edge. The thresholds can be estimated by statistics gathered from a small calibration dataset. Combining topology, bits and thresholds, we can genereate the simulated graph and evalute it on the calibration dataset (around 128 samples). With the output/accuracy as the feedback, the learning algorithm then can select the next set of bits setting.
In the end, with the best strategy found during search, we will realize the simulated model to the real low-precision integer model.
Specification: bit, threshold, scale
In this section we will introduce serveral importance notations: bit, threshold, scale.
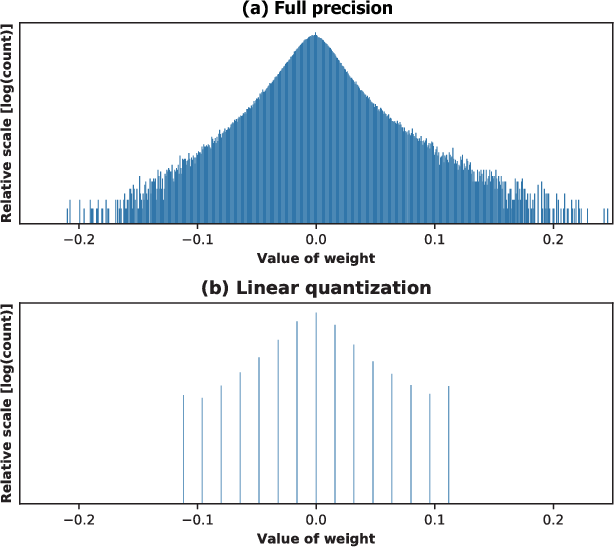
In general, the goal of quantization is to transform a graph running with floating point number (real value) to a graph running with integer numbers (quant value), without sacrificing too much accuracy. So given a tensor with real values, what the realation with its transformed quant value? Here is the specification we will follow in current implementation:
scale = threshold / pow(2, bit - sign_bit)
QUANT_VALUE * scale = REAL_VALUE
REAL_VALUE / scale = QUANT_VALUE
bit is the number of bit we will use to represent the real values. Notably, it does not necessary to be the bit of the data type exactly: even we choose int8 data type, we can still only use 6 bit. This is useful in some condition that opeartor’s output requires inputs to be fit in small range. Threshold is a estimation for range of real value, which can be the max value range simply. There also exist many complicated threshold estimation methods for better accuracy, which will be discussed in the threshold esimtaiton section.
Hardware Description
The hardware description is trying to provide a central abstract for hardware properties we need to consider during quantization. By declaring those properties first, we can avoid to handle hardware specifc condition in followed quantization steps.
Currently we can specify input data types, and output data types of every operator.
desc = Hardware()
desc['add'].append(OpDesc(in_dtypes=['int32', 'int32'], out_dtypes=['int32']))
desc['add'].append(OpDesc(in_dtypes=['float32', 'float32'], out_dtypes=['float32']))
desc['nn.conv2d'].append(OpDesc(in_dtypes=['int16', 'int16'], out_dtypes=['int32']))
desc['nn.conv2d'].append(OpDesc(in_dtypes=['int8', 'int8'], out_dtypes=['int32']))
desc['nn.global_avg_pool2d'].append(OpDesc(in_dtypes=['float32', 'float32'], out_dtypes=['float32']))
The hardware information has been utilized serveral times during the whole procedure:
- By specifying operator only support float computation, the system will realize a end need to be put before the operator. This should be able to address some problem for VTA pipeline, we would like to specify some operators to be run with integer instruction on VTA core and some operators with float instruction on the normal cpu.
- The bit choice space is generated from it. For every edge, we can infer that the maximum bit we an use depends on the data type constraints.
- After we decided the number of bit will be used on every edge, we will select proper data type according to the hardware information.
More property will be added depends on our need in the future development.
Simulation
Threshold Estimation
In order to estimate the threshold, we will run the model on the calibration dataset first, and collect the statistics we need. Currently we will save all the outputs of intermediate operators. To determine the threshold from the collected outputs, there exist several strategies:
- max_range: use the maximum value of the output as threshold of the corresponding node.
- power2_range: round the maximum value to the nearest power of two value as the threshold.
- kl_estimate: choose a threshold which will make the KL distance between real output and quantized output small enough.
Currently I choose the power2_range method, which makes it possible to use shifting to replace multiplication and give us better performance in the final quantized model. Although kl_estimate will give us the better accuracy, but it is quite time consuming, which is not feasible for using during search currently.
One tricky problem is that for operators like addition, which only can be executed while its operands’ scales are eqaul. We would like to unified its operands’ scale first. To achieve this, estimated thresholds will be adjusted before simulation. I have introduced a transform named threshold_rectify and a operator specific attribute for it:
@register_fthreshold_rectify('add')
def threshold_rectify_for_add(in_bits, out_bits, in_tholds, out_tholds):
# choose scale of the one with maximum threshold
idx = np.argmax(in_tholds)
unified_scale = in_tholds[idx] / (2**(in_bits[idx] - sign_bit))
# adjust thresholds according to the unified scale
...
Simulated Quantize
Given bits and thresholds, now we can try to generate a model to simulate the errors brought by quantization. After analyzing, we can found that the error comes from serveral aspects: 1. rounding error; 2. saturated error; 3. overflow error.
We will insert a simulated_quantize operator on every edge, which is trying to simulate those errors. The definition has been attached as below:
def simulated_quantize(data, in_scale, out_scale, clip_min, clip_max, in_dtype, out_dtype):
if in_dtype == 'float32' and out_dtype == 'float32':
# no need to quantize
return data
# simulated overflow error
data = data / in_scale
data = topi.cast(data, in_dtype)
data = data * in_scale
scaled_data = data / out_scale
# simulate saturated error
clipped_data = topi.clip(scaled_data, clip_min, clip_max)
# simulate round error
rounded_data = topi.cast(topi.round(scaled_data), out_dtype)
out = rounded_data * out_scale
return out
So how to calculate those parameters by bit and threshold? out_scale, clip_min, clip_max are pretty straigt forware:
integer_range = 2**(bit - sign_bit)
out_scale = threshold / integer_range
clip_min = - (integer_range - 1)
clip_max = integer_range - 1
For in_scale, in_dtype, out_dtype, we need to do extra effort to infer them.
Scale Inference
we can found in the model above, the in_scale of SimQ is actually the scale of previous operator’s output, which can be calculcated depends on the operator definition. We providing a register function for such property:
@register_finfer_scale('nn.conv2d'):
def infer_scale_for_conv2d(in_scales):
return in_scales[0] * in_scales[1]
Data Type Assignment
For data type, we will traverse operators, select operator specification from the hardware description that satisfy the in bit and out bits requirement.
Learning
With all the preperation decribed above, now the quantization problem is converted to a learning problem: we want to find the best setting from the choice space, to achieve the best accuracy (or other objective like performance) of simulated model, and we can use the output(accuracy) every round as the feedback.
For this learning problem, I have implemented random_search, simulated_anealing, also a greedy algorithm. Currently my experiemnt shows that greedy search is the most feasible one.
Log Format
Since the search space is quite large and the searching procedure can be quite long, it would be better to have a formal log format to record the experiment details for reproducibility and exchangeability. Currently I choose json format, and the detail is show as below:
- version: the log format version.
- strategy: the quantization strategy.
- model_hash: the hash value of the model, can be used to verify whether the model match the strategy.
- topology: the topology of the quantized model
- node_conds: which nodes will be quantized
- edge_conds: which edges will be quantized
- bits: number of bit on every edge.
- thresholds: threshold for every node output.
- results: the result of experiment
- sim_acc: the accuracy of simulated model
Search Speed
Realization
After getting the best quantization strategy: topology, bits, thresholds realizing the simulated graph to the low-precesion quanitze graph is pretty stragiht-forward. We just need to replace the SimQ op on every edge with low-precision integer operations.
Debug
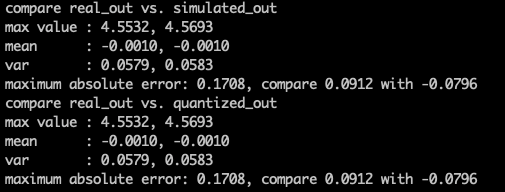
The most painful thing is to debug where is wrong with my quantized model, since usually we only know that thefinal accuracy is pretty bad. I have implemented a inspect_graph_statistic function to check statistic difference before and after quantizing layer by layer, so that I can locate where is wrong quickly. It is demonstrated quite helpful during my development.
API Demo
from tvm import hago
# ideally we will have predefined description for x86, arm, gpu and vta
hardware = hago.create_sample_hardware()
strategy, sim_acc = hago.search_quantize_strategy(graph, hardware, dataset)
quantizer = hago.create_quantizer(graph, hardware, strategy)
simulated_graph = quantizer.simulate()
quantized_graph = quantizer.quantize()
Current Status
I have made the whole pipeline worked and get a preliminary 68.7% result on resnet18_v1, noticed that here I did not skip the first convolution layer and only use power-of-two range instead of kl distance, there should be much more room to improve.