[RFC][Quantization] A new quantization framework in TVM: initial RFC (1/4)

Development pre-RFC
#1

A new quantization framework in TVM: Initial RFC

In this and subsequent RFCs, we will present a new framework for doing static, data-aware quantization on relay graphs.

Previously, I put up an RFC to discuss the new quantization framework in TVM. After that RFC, I got some feedback from the community on the design, and also heard that community members would like to see the design split up into multiple RFCs. This RFC addresses that feedback, but still aims to stand alone from the previous RFC.

Since this is an introductory RFC, it will go over the conceptual structure of the project, but will not go into class definitions or implementation details. Those details will be provided in three future RFCs: one on pattern-based rewriting, one on choosing quantization parameters and one on creating the final quantized graph for inference. The future RFCs will correspond directly to the subsections of the “Outline of this Work” section of this RFC.

Motivation for a new quantization framework in TVM

The current quantization framework has proved difficult to extend and modify: adding new features requires changing many different files and passes. As a result, supporting quantization of complex graph structures, supporting many calibration methods, and adding multi-precision quantization is difficult.

In this work, we aim to create a modular and extensible framework that can be easily modified and maintained.

Background and Prior Work

This work relies on concepts developed in relay’s QNN (quantized neural network) ops, and even uses some QNN ops. If you are not familiar with QNN, it may be helpful for you to read about QNN before continuing. The code is here. QNN uses quantization parameters to quantize data to a target datatype. For example, qnn.quantize takes in data in FP32, a scale, a zero point and an output dtype, and returns a quantized value that has been appropriately scaled, shifted, clipped and cast to the target datatype.

We use the Relay pattern matcher to do a lot of our rewrites, and we assume some level of familiarity with it throughout this document.

Flavors of quantization and a few definitions

There are many different ways to approach quantization. For the purposes of this RFC we focus on affine quantization:

Q = clip(s * (A - z), dtype)

where A is the value we are quantizing, s is the scale, z is the zero point and Q is the clipped value. In this scheme, the scale is always a float and the zero point is an integer. We’ll refer to the scale, zero point, and output datatype as the quantization parameters.

After data has been scaled, shifted and clipped using quantization parameters, we say that that data is in affine space. If we reverse the scaling and shifting, the data has been moved back into real space. Affine spaces are defined by quantization parameters (e.g. scale and zero points) which map values back to the real numbers.

We say that we are changing from one affine space to another (e.g. “requantizing”) if we change data expressed with one set of quantization parameters into an approximation expressed with a different set of quantization parameters.

There are also many different ways to quantize models. These include quantization aware training, data-aware quantization, dynamic quantization, and multi-precision quantization.

Quantization aware training involves training the network while simulating the effects of quantization, so the network learns how to deal with data loss. Often, quantization aware training is the most accurate approach. However, it requires training the network, which TVM does not currently support.

Multi-precision quantization involves quantizing different parts of the graph as different datatypes.

Dynamic quantization inserts code into the original graph to calculate appropriate quantization parameters at runtime. The advantage of dynamic quantization is that we don’t need access to a representative dataset to calculate the scale and zero points. Additionally, it is usually more accurate than data aware quantization since we can pick optimal quantization parameters for one particular set of inputs. For memory-bound models (e.g. ones with lots of parameters) dynamic quantization can still see major savings in latency and power. As a result, it is popular to use dynamic quantization on NLP models. However, calculating quantization parameters at runtime introduces runtime overhead that will affect the performance of the final graph.

Static data aware quantization uses a representative dataset and intermediate values from the inference graph and/or an approximation of the quantized graph to pick appropriate scales and zero points. This representative dataset only requires the data which is fed into the model and does not require ground-truth labels. It involves inserting relay operations to simulate the effects of quantization while examining intermediate operations to determine the optimal quantization parameters.

In static data aware quantization, we may want to pick our quantization parameters using intermediate values from an approximation of the quantized graph. There are two common methods to do this: simulated quantization and fake quantization.

Simulated quantization transforms data into affine space using quantization parameters, but does not cast to the target datatype-- instead, the output of simulated quantize is in FP32. Note however, that the values of a tensor are still integral. FP32 should be able to express integral values in the range of 24 bit integral types which we believe will be more than enough for almost all applications. Simulated quantization functions are already written and were introduced in this PR.

Fake quantization simulates the data loss that would occur during quantization, but does not return a tensor in affine space. Fake quantization is the method used in TensorFlow’s QAT (quantization aware training).

Goals and scope of this work

The main goal of this work is to implement an extensible framework for static data-aware quantization. We’ll use simulated quantization to provide intermediate values we can use to choose quantization parameters.

In this initial work, we’ll support quantization to int8 and also fall through to fp32 (i.e., if quantization of part of the graph results in a particularly large accuracy loss, we can revert that part of the graph to fp32). Additionally, the algorithm to choose scales and zero points will be implemented in Python instead of Relay. This will allow us to support many different methods of choosing scales and zero points, and allow us to add more methods easily. We aim to make the graph rewriting process robust enough to support quantization of complex graph structures.

Additionally, we would like to lay the groundwork to support dynamic quantization and multi-precision quantization. Dynamic quantization is implementable under this suggested framework, and multi-precision quantization could also be supported. However, this is future work, and we won’t go into too much detail here.

We’ve chosen to focus on static data aware quantization because TVM does not have training yet, so we cannot attempt to support quantization aware training. Additionally, the runtime overhead in dynamic quantization can be significant.

We’ve chosen to use simulated quantization instead of fake quantization because simulated quantization allows us to examine the effects of lower-precision accumulation datatypes, and specifically avoid quantization parameters that cause integer overflow. Since int8 quantization uses int32 accumulation, we don’t need to worry about integer overflow in this initial work. However, some hardware accelerators use lower-precision accumulation datatypes-- for example, an FPGA may multiply two int8 values and accumulate them into an int14 datatype. In those cases, simulating integer overflow will be useful.

Outline of the work

For this and future RFCs, I have split the work into three conceptual chunks: pattern-based rewriting of the graph, choosing quantization parameters, and then creating the final graph by combining different affine regions. Each of the subsections below will correspond to a future RFC. Because there will be future RFCs, in this section, I aim to present a conceptual overview of the approach, but I will not provide too many implementation details here. If you have any questions or if there is anything I can clarify at this point, though, please feel free to ask.

Pattern-based rewriting

We use the pattern matcher to identify subgraphs that we would like to quantizeand pick scales and zero points for. Initially, we’ll support quantizing these patterns using the pattern-based rewrite: nn.conv2d, nn.conv2d → nn.bias_add, nn.conv2d → add, nn.dense, add, subtract, and multiply, however, adding new patterns is not difficult.

For each pattern we’d like to rewrite, we provide two rewrite callbacks which transform the pattern into affine space.

One rewrite callback rewrites the graph to a simulated quantized version of the pattern, using the qnn.simulated_quantize and qnn.simulated_dequantize ops to transition into and out of affine space. We insert Relay variables as the scale and zero points. The simulated quantization graph is then used to calibrate the quantization parameters of the graph.

The second rewrite callback rewrites the graph to the quantized inference graph. (This rewrite will be done after we pick the scales, zero point and the datatype we want to quantize the pattern with). In this rewrite, we use qnn.quantize and qnn.dequantize to move in and out of affine space. This is the graph that will be used for running the final graph.

We are committed to using qnn.quantize, qnn.dequantize, qnn.requantize, qnn.simulated_quantize and qnn.simulated_quantize. However, it’s not clear what the best way to handle the quantized versions of more complex operators, like nn.conv2d and nn.dense. (Doing a convolution or dense operation in affine space adds extra terms created by the zero points, so we then have to subtract these terms off to be consistent with the result of the original operator. See tvm/convolution.cc at main · apache/tvm · GitHub for an example of how current QNN ops deal with this problem.)

We have a few options:

  1. Handwrite the affine versions of nn.conv2d and nn.dense directly in the rewrite callbacks, in Python. We would make utility functions that create the affine-space AST given input datatypes and accumulation datatypes.

This option is the most flexible, and least invasive to existing code in QNN. If we want to support more operators using this pattern-based rewrite, it’s easy to write them directly. We don’t have to worry about writing new Relay ops.

However, this option does duplicate some of the functionality of QNN, and creates a split between the infrastructure used for automatic quantization and importing pre-quantized graphs. Additionally, hardware companies find the symbolic nature of QNN useful, since they like to offload qnn.conv2d → qnn.requantize onto accelerators. If we don’t use QNN, they will have to match larger relay patterns to offload, and additionally will need to support both QNN and this new method.

  1. Extend qnn.conv2d, qnn.dense, etc. to be used with more datatypes, including fp32. We would also have to add an attribute to QNN specify the accumulation datatype used.

In this option, qnn.quantize, qnn.dequantize, and qnn.requantize will only ever be used for inference graphs, and qnn.simulated_quantize, qnn.simulated_dequantize will only be used in calibration graphs. However, all other QNN ops (qnn.dense, qnn.conv2d, etc.) can be used in both the final inference graph and in the calibration graph.

These QNN ops would be used in both the simulated quantized graph for calibration and the inference graph, but with different datatypes.

The advantage of this option is that it uses the same infrastructure as the importer that imports quantized graphs.

However, it will require a significant rewrite of the backend of QNN. And, it is slightly less flexible–if we want to support quantization of more quantized operators, we will have to implement them in QNN before using them with the pattern matching system.

We prefer the second option presented here because it unifies auto quantization with the existing quantization importers. We also considered introducing qnn.simulated_conv2d, qnn.simulated_dense, etc. However, we don’t think that this is necessary since these ops would be purely symbolic. Graphs that are simulated will have qnn.simluated_quantize and qnn.simulated_dequantize in them, so it will be easy for users to tell calibration graphs from inference graphs. It would be great if we could get some feedback from the community about these options, and about the direction to take QNN in.

Let’s take a look at an example using the second option.

754×1158 37 KB

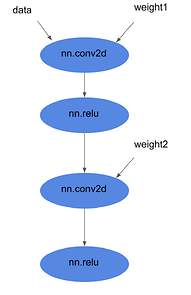
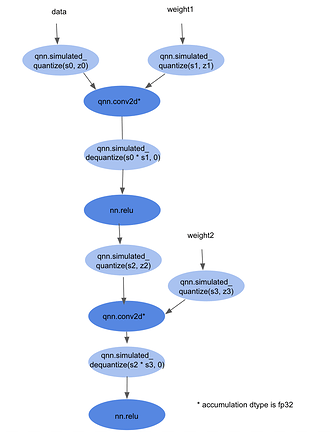
Let’s consider this graph. When we do our pattern-based rewrite, we end up with a graph that looks like this:

962×1242 75.7 KB

We’ve inserted Relay variables in place of all the scales and zero points, and do the convolution calculations in affine space, though the accumulation datatype of the qnn.conv2d ops is fp32, not int32. Additionally, we’ve left nn.relu in real space for now.

Choosing quantization parameters

After rewriting the original graph to simulate quantization, we run a calibration loop in python to pick the quantization parameters. It will run the simulated graph many times, and choose the quantization parameters in topographical order (i.e., it will pick the first scale and zero point, then the next scale and zero point, etc). We will use intermediate values from running E1 to choose the quantization parameters. We will support per-channel scales.

There are many different methods for picking scales and zero points, including KL-divergence, 99% of the maximum value of the input tensor, averaging the maximums seen in input tensors. Because of this, we want to make it easy to change the method of picking scales and zero points. So, the actual method used to calculate scales and zero points from data will be a python callback that is passed into the calibration loop.

This will make it easy to add more methods of picking scales and zero points without refactoring the rest of the code. There will be an additional RFC on the details of how this will work.

Creating the quantized graph for inference

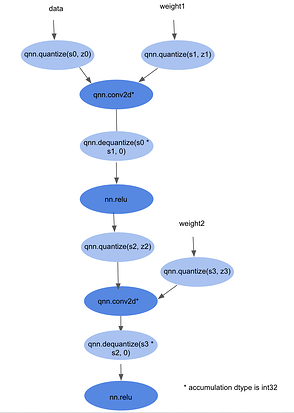
We create the quantized inference graph in two steps. First, we do a pattern-based rewrite on the original graph to transform each pattern to the quantized inference version of that pattern. To do this rewrite, we need to have determined the values of scales and zero points.

The output of this rewrite will look very similar to the simulated quantized rewrite, however, the accumulation datatypes will be int32 instead of fp32, and we will insert qnn.quantize and qnn.dequantize instead of qnn.simulated_quantize and qnn.simulated_dequantize. After this transformation, the graph will look something like this:

880×1236 66 KB

Note that after the pattern-based rewrite, there will be portions of the graph that remain in real space. For example, all of the nn.relu ops in the graph pictured above are in real space and still operate on FP32 datatypes. However, to get the most speedup, we want to avoid operating in FP32 as much as possible.

To solve this problem, we’ll expand the regions of the graph that are in affine space by pushing qnn.quantize and qnn.dequantize through the surrounding ops. When we push qnn.quantize and qnn.dequantize through other ops, we will transform the other ops to be in affine space, if possible. To do this, we’ll have an allow_list, which is a mapping between a Relay op and how to transform it into affine space. If an op is not on the allow_list, we will not push a qnn.quantize or qnn.dequantize past it.

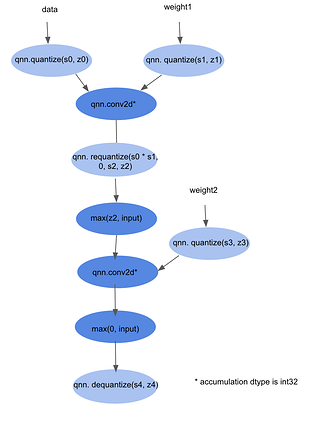
For example, consider moving qnn.quantize up past the first nn.relu in the graph above. This qnn.quantize has a scale s2 and zero point z2. To maintain correctness of the graph, we need nn.relu to take the shift by z2 into account. Therefore, we transform the nn.relu into max(z2, input).

Finally, we consolidate adjacent qnn.quantize and qnn.dequantize ops into qnn.requantize ops. Because we’ve moved the qnn.quantize ops and qnn.dequantize ops around, most of them should be adjacent. The only ops between qnn.quantize and qnn.dequantize should be ones not on the allowed_list, which cannot operate in affine space anyways.

The final graph will look like this:

860×1152 62.9 KB

Please note that this rewrite is very complicated, and we have only provided a very brief overview of it here. There will be another RFC on this specifically to break down the steps involved.

Bottom-up approach versus top-down approach

The method we presented for quantizing graphs is a “bottom-up” approach. We do the local rewrites before doing the graph-level rewrites. Specifically, we decouple inserting qnn.requantize ops from the pattern-based rewrites.

Most existing quantization frameworks use a “top-down” approach-- they start with the global, graph level rewrite and do more local rewrites as they go.

There are benefits and drawbacks to both approaches.

A big benefit to the bottom-up approach is that it is more generic. We can easily add new patterns without changing the calibration methods and without changing the final rewrite that inserts qnn.requantize ops. In the top-down approach, we would need to embed the lower-level rewrite of patterns into the more global, graph based rewrite. This makes the top-down approach more ad-hoc less modular than the bottom-up approach.

One downside to the bottom-up approach is that we get slightly less control over the placement of qnn.requantize ops with respect to other QNN ops. Let’s consider an example: a hardware vendor wants to offload qnn.conv2d → qnn.requantize to an accelerator. Because we do not explicitly place the qnn.requantize op after the qnn.conv2d op, we have to rely on a separate pass to combine qnn.quantize and qnn.dequantize correctly, and to transform all ops in between them into affine space. Additionally, that pass has to put qnn.requantize in the correct spot relative to qnn.conv2d so that the pair of ops can be offloaded correctly.

We acknowledge that this logic is complex. However, in the top-down approach, we would have to implement similar logic that is similarly complex. Inserting qnn.requantize directly after patterns requires knowing the quantization parameters of the output tensor. In cases where the graph does not branch, this is not too difficult, but does force our rewrite to be less modular. However, if the graph branches, we have to figure out what the input quantization parameters are to all the branches, which requires global reasoning about the graph and its structure.

There are similar technical challenges in both approaches, and a top-down implementation would probably work just as well as a bottom-up implementation. We favor the bottom-up approach because it is more generic, modular and extensible.

Future RFCs

Each of the steps outlined above is complex, and we did not go into very much detail in this RFC. For readability and ease of communication there will be three more RFCs that go into more detail. One will correspond to each of the subsections of the “Outline of this Work” section, as these are the most complex parts of the framework:

  1. The pattern-based rewrites and updates to QNN
  2. Picking quantization parameters
  3. Creating the quantized inference graph and expanding affine spaces

Future work

In the future, we would like to support multi-precision quantization. We are specifically interested in allowing fallback to fp32 if quantizing a portion of the graph in int8 causes a large degradation in accuracy. And, we would like to add support for int4 quantization. Additionally, we would like to support dynamic quantization, as defined earlier in this RFC.

We have designed this framework with implementing multi-precision quantization and dynamic quantization in mind, so we will not have to do any major rework of the work presented here to support these features. However, we view these features as extensions of the work presented here, so a discussion of these features will not be included in the initial set of RFCs.

Thanks to @AndrewZhaoLuo, @mbrookhart and @masahi for helping edit this RFC

16 Likes
Do TVM support quantilization itself?
Relay quantization: "TVMError: AssertionError: assert isinstance(expr.args[0], _expr.Constant)"
#2

@mbaret @anijain2305 It would be great if you could take a look and let us know what you think!

#3

This looks like great work, thanks for the RFC!

I agree that it’s very valuable for there to be a stage in the Relay lowering where the ‘QNN-ness’ is explicit - we’ve got both hardware and performance libraries which accelerate quantized operators specifically.

One of the things that complicates our ability to match QNN operators though is the inconsistent way they’re represented. For instance, for QNN convolution we must match qnn.conv2d -> bias_add -> qnn.requantize whereas for something like sigmoid we must instead match qnn.dequantize -> sigmoid -> qnn.quantize. This broadly corresponds to the difference between QNN ops that have ‘native int8’ support and those which are faked through fp32.

So with regard to your suggestions about how we can do pattern-based rewriting, I wonder if we could consider a 2-stage rewrite. A first one which would turn convolution into ‘faked int8’ convolution (qnn.dequantize -> nn.conv2d -> qnn.quantize) and then a second pass which rewrites that into the proper int8 quantized convolution (skipping qnn.conv2d). The first form would be a good target for hardware off-loading and the second might avoid some of repetition you’ve described.

Status on quantization in TVM
#4

@mbaret Thanks for the input!

As I understand it, you are proposing producing a fake quantized graph, which then can be used for calibration. Additionally, hardware vendors would be able to directly pattern match on this graph to do offloading to hardware targets. Finally, we’d have a pass to generate the final relay version of the graph from the original and/or the fake quantized graph. (Please correct me if I misunderstood!)

You said that you’d prefer matching qnn.dequantize -> nn.conv2d -> qnn.quantize over matching qnn.quantize -> qnn.conv2d -> bias_add -> qnn.requantize.

One question I have for you is what the exact pain point is in the inconsistency of how quantized graphs are represented. Is it the presence of multiple ops in the affine space? (Would qnn.dequantize -> nn.conv2d -> nn.bias_add -> qnn.quantize be OK?) Or is it that you have to deal with both qnn.requantize as well as qnn.dequantize and qnn.quantize? (i.e., matching on a graph that has no qnn.requantize ops in it would be better for you)

Also, I’m curious what you’re replacing the qnn.dequantize -> sigmoid -> qnn.quantize with. Are you moving the sigmoid into int8, and requantizing right after the sigmoid? Is the problem here that you are having to match and offload qnn.conv2d, qnn.dense, and other ops that are already in affine space, as well as dealing with ops that have not correctly been moved into affine space?

#5

The inconsistency pain point is interesting. I had a similar problem with matching against dequantize → resize → quantize. I had to extract input qparams and output qparams from dequantize and quantize respectively, since there is no qparams attached to resize.

To improve on the current situation, I would rather enrich qnn ops to include those ops that are currently wrapped with dequantize/quantize, rather than completely skipping qnn.conv2d and qnn.requantize and make everything wrapped with dequantize/quantize. We can hide dequantize and quantize in the default QNN lowering path, and BYOC people can directly match against quantized sigmoid etc with qparams explicitly attached to it.

The pros of that approach would be:

  • We can keep the same representation and patterns for prequantized and auto-quantized cases
  • Patterns are simpler (no need to match against dequantize and quantize)
  • BYOC backend can directly extract qparams from the arguments of a target quantized op, rather than from surrounding dequantize and quantize.

The con would be more work on QNN, but I think adding a new q op that have previously been dealt with by dequantize and quantize would be a mostly mechanical process that could even be automated (e.g. with a macro). Moreover, I think the list of such ops is not big, sigmoid, softmax, resize, and maybe hswish.

#6

@masahi I agree, I think that if there are not that many ops we need to do this for, adding them to QNN would be ideal.

I also think that we could deal with replacing qnn.dequantize -> sigmoid -> qnn.quantize with a qnn.sigmoid op fairly easily using the pattern matcher. We could probably build this into our final rewrite step easily. Additionally, directly adding the qparams to these ops is a good option because some of the QNN ops already require them.

One question I have, though, is whether we should be choosing qparams for these ops instead of using ones from the previous quantized pattern.

If we write qnn.resize, qnn.sigmoid, etc., then we can quantize these using the pattern-based rewrite, and choose qparams for these ops. So initially we’d rewrite to qnn.quantize -> qnn.sigmoid -> qnn.dequantize, choose the correct qparams, and then in the final graph, we’ll end up with qnn.sigmoid -> qnn.requantize, which is consistent with what happens after quantizing a convolution

#7

Yes this sounds good, in that we can quantize sigmoid etc just like other ops like convolution. Probably we don’t need requantize for sigmoid and most other ops that are currently wrapped with dequantize / quantize.

1 Like
#8

We have accelerators that directly support quantized int8 → int8 sigmoid with any requantization handled, so we can lift this full pattern and map it directly to a hardware operation.

I can perhaps elaborate about what I mean on consistency. qnn.conv2d behaves a bit differently to, say, qnn.add. For qnn.conv2d, the type of the function is int8 → int32 and the result is in some intermediate quantization space, whereas qnn.add is straightforwardly int8 → int8. Additionally, when qnn.conv2d was first added to TVM it didn’t include the input and weight scales separately as due to a mathematical quirk the only quantization parameter you needed was the input*weight scale. We can see this in the documentation which explains that the input/kernel scale were added just to help support accelerators:

    input_scale: tvm.relay.Expr
           The scale for the input tensor. The scale for the input tensor is
           stored purely for convenience here. See more commentary below.

    kernel_scale: tvm.relay.Expr
           The scale for the weight tensor. The scale for the weight tensor is
           stored for access to this during relay. This information is not
           needed in the pass pipeline after qnn.conv2d is lowered to the
           sequence of steps as in nn.conv2d. See also input_scale in Requantize.

This would have been simpler to reason about with ‘fake quantization’ where to determine the quantization parameters of any of the inputs/outputs we can just visit the appropriate quantize/dequantize op and read off the QNN params in a ‘unified’ way (i.e. we don’t need to have different ways of extracting QNN information for every operator).

On the second point, we’ve recently been going through an exercise of trying to come up with patterns to match all the various quantized operators and it’s been pretty painful. Aside from the 3 conventions already discussed (int8->int8 QNN ops like qnn.add, int8->int32 QNN ops like qnn.conv2d and fake QNN ops like sigmoid) there are also other interesting patterns like:

  • avg_pool2d gets a cast before and after
  • mean becomes cast → mean → qnn.requantize
  • some ops do nothing at all (pad/max/min)

So to a degree here we are at the mercy of the authors of the framework frontend as to how they choose to express quantization. On the other hand, if the frontend simply inserted dequantize/quantize where ever it saw a quantized tensor in TFLite we’d have a very consistent and hopefully more stable representation to match and offload against. Clearly though there’s a downside to this in increasing the complexity of any subsequent QNN lowering pass.

Apologies for the wall-of-text :slight_smile: Having said all this I think if we can ‘standardize’ the QNN ops of Relay and ensure broad coverage that would probably provide similar benefit. The most valuable thing for pattern matching is just that there exists a canonical representation of QNN, so switching to either quantize/dequantize or QNN ops would be an improvement for us.

1 Like
#9

+1 for a standarized stable Relay representation of QNN operators! From the hardware accelerators point of view, we have the problem that every frontend lowers the quantized models into Relay however they like, so as an example, we would need different patterns for Relay from TFLite and from PyTorch. So some sort of stable representation would be really useful indeed.

It is not entirely clear to me what’s the position of this RFC on this, do you plan to have a stage where the Relay would resemble to the Relay e.g. TFLite frontend generates (so it could be picked up by current pattern matchers) or to add a completely different Relay representation for auto-quantization or to change the way frontends currently lower to Relay to match the auto-quantization Relay?

(Btw, very well written RFC on a very complex topic!)

2 Likes
#10

Thank you for this very well written proposal. I’m fully in support of your proposal and have been working on similar ideas. From an implementation point of view, the framework should be flexible enough to handle op specific quantization patterns. For example, various modes of a conv2d may need different quantization schemes. Some hardware may benefit from different quantization schemes due to more efficient instructions.

As the proposal mentions there are many ways to minimize quantization error in the litterature. We should design this framework with that scalability in mind.

It should also be possible to get statistics.

1 Like
#11

I agree this is quite important. To add a specific case that’s causing us some trouble at the moment, qnn.requantize is implemented differently in Relay to the quantization scheme in TFLite and therefore we can get quite different results running a network through TVM vs. TFLite. For a single operator this tends to just be an error of +/- 1 from rounding mode differences but propagated through a large network we’ve seen these errors add up.

I think either we need qnn.requantize to be ‘configurable’ to support the different numerical behaviour of different frontends or potentially have different requantize ops entirely.

1 Like
#12

I haven’t taken a close look at what the TFLite / Pytorch importers do. I agree that it does seem suboptimal that they are creating different patterns, but I don’t think that rewriting these importers is within the scope of this work. However, I can try to create more consistency within this framework, and then hopefully this consistency can be extended to the importers in the future.

Regarding this:

QNN ops are symbolic, so the actual Relay code that gets run is specified in Canonicalize functions (qnn.requantize also has a Lower function attached to it, and I’m not clear on when the Canonicalize function is used and when the Lower function is used in this case…)

We’ve thought about moving the Canonicalize/ Lower functions to Python… Then, it would be easier to change these backends in the future. And we could maybe have mulitple canonicalization functions for emulating different backends. I’m not sure how dispatching to these different functions would work, though.

I think that the pain point you are describing is a fundamental problem with doing multiple pattern-based rewrites in a row. The first rewrite is a mapping from pattern to AST. Then when you try to do the second rewrite, you need to write a new pattern that matches all the ASTs produced from the first rewrite. You might be able to generate a pattern from the code that produces the AST… but that’s a pretty complex program analysis / synthesis problem.

A potential solution is you could ingest the graph before we’ve inserted qnn.requantize – so basically, we will have only transformed specific patterns into affine space (like qnn.conv2d -> nn.bias_add), and we could guarantee stability of the AST of a certain number of these patterns, so you won’t need to write that many.

Additionally, we won’t have transformed any of the other ops to run correctly in affine space at this point, so you could just offload those directly instead of trying to match the AST they’ve been transformed into. (This doesn’t solve the problem of knowing what the qparams are for these intermediate ops, though… I need to think about that more.)

1 Like
#13

Yes, I feel your pain, having worked on supporting both PT and TFLite for a BYOC backend. I’d say the difference in PT- or TFLite-derived QNN graphs are inevitable to some extent, due to the different ways quantization work and how quantized operators are implemented in each framework.

I think this point is one of the reasons auto quantization in TVM could be interesting for BYOC people that are already using QNN for prequantized models. We get QNN graphs consistently for each framework models and do not have to deal with idiosyncrasy of different ways quantziation is done in each framework.

It is not clear how auto-quantized QNN graphs are going to look like, hopefully BYOC people can reuse the same patterns that they already have for PT or TFLite.

3 Likes
#14

I think this is orthogonal to this work, we can separately discuss e.g. adding a new attribute to requantize to support different modes (fixed point vs float math etc) @anijain2305

3 Likes
#15

Yes exactly! I feel your pain too :wink: Some frameworks use full range eg [-128,127], others restricted [-127,127]. Even at operator level, using per-channel or per-layer is sometimes not sufficient. A point convolution should not deal with channels the same way a generic conv do. Likewise for a conv with groups etc. or even more fun with fusing/splitting operators.

So the framework should be flexible to use such dedicated quantizers if need be, maybe through some kind of pattern matching.

I like to use the video codec analogy: there are many ways to encode a video but you must have one way for any player to play it back.

In that sense, I see qnn ops as the decoder part, and this framework flexible enough to allow various encoding schemes over time. For validation, we could start with reproducing say TFlite way but we should not be limited by it (because TFlite is very very limited).

1 Like
#16

Agreed, but it would be nice to agree a ‘TVM’ standard way to represent quantization at various levels. That way others (maybe even me :slight_smile: ) can start applying that standard to the frontends. It would also make it easier to get accelerators to work with TVM’s auto-quantization.

We need to be a bit careful doing this, because it’s the frontend behaviour that’s different rather than the backend. So any such differing in canonicalization should correspond to an attribute on qnn.requantize that determines the desired numerical behaviour.

I think this is one of the major complications for quantized accelerators - we require that everything is in the affine space. That is to say, we don’t have an ‘integer’ accelerator but specifically a quantized one. So even things like sigmoid which seems strange to run in the affine space at least need to be ‘fake quantized’ with dequantize/quantize so we have access to those affine parameters. TFLite does this relatively neatly by having the quantization parameters as part of the tensor type but unfortunately we can’t do the same thing in TVM.

I’m also hoping for this :slight_smile: If we can arrive at a durable and flexible representation for auto-quantization I think it would even be beneficial to see if we can rewrite parts of the TFLite frontend to conform to that.

1 Like
#17

Right, my point here is that the challenge you are encountering is that the quantization framework translates normal Relay ops into affine space (which sometimes is multiple Relay ops), and then you have to match the affine space version of the Relay op that the framework created, which is tricky. Really what you want to do is know what the QParams are and just offload the original Relay op without worrying about what the affine space version of the Relay op is.

I’m not sure what the best way to solve this is, though.

You could make a ton more symbolic QNN ops that store the QParams directly, but then you end up in a situation where you need to make QNN corresponding to most Relay ops, which doesn’t make a ton of sense.

Or we could do something like insert qnn.requantize ops and change the dtype of all the intermediate ops to be int8, and annotate all the intermediate ops with their QParams, so you could match those ops directly and offload them. This graph wouldn’t be correct because Relay ops like sigmoid wouldn’t take QParams into account, but it wouldn’t matter because you’d just replace them with your kernel, which does take the QParams into account.

#18

Lots of interesting thoughts here. Overall it seems the main pain point is that it’s really hard to match quantized operations to do BYOC or something similar. I do think a more “unified” relay representation is the way to do this and this work can certainly lay the foundation for that. Here are my thoughts on this:

I think a major issue with quantized operations vs. non-quantized operations in general is how much rounding matters. If you lose 1 out of 4 bits of information it can be really significant. Therefore, implementation details matter a lot more than FP32 case because they can change how rounding is done and therefore affect the semantics of the operation in a more meaningful way. As an example, we can imagine doing a quantized convolution and bias-add operation either by taking the accumulation buffer of the convolution and using that for the bias-add or downsampling the accumulation buffer to 8 bits and using that for the bias-add. Obviously the first one is preferable but maybe you have hardware which can only do the second. We therefore have to be able to support both in QNN.

The main point is that while conv2d represents a mathematical operation which is well defined, qnn.conv2d really needs to represent a family of mathematical operations each of which approximates conv2d in a different way. Right now what we’re running into I believe is the fact that qnn.conv2d is very specific and doesn’t provide enough knobs to change the semantics of the operations.

Keep in mind that I’m not familiar with a lot of the examples that @mbaret makes but it seems to me that a lot of these problematic patterns have to do with getting things to the correct input types for QNN ops. We can easily imagine a world where these QNN ops can take in really any input pattern and internally when things are lowered things are cast to the correct type. In the case of a conv2d we might imagine a conv2d-bias-add block with some sort of knobs exposed that might specify how the add after the conv2d is performed. We then wouldn’t have these scattered requantized, cast, etc. which might make the pattern matching for BYOC easier.

I know fused operator nodes aren’t really very relay-y but then again QNN isn’t normal relay since as mentioned before, QNN.conv2d needs to really represent a lot of different operations. The potential downside is having an explosion of potential fused operator nodes. However I argue that every fused operator node is just a case with special implementation details which we would have to deal with anyway.

Basically, it seems if we want nice pattern matching off the QNN graph, we have to avoid leaking implementation details to the QNN relay graph. We still need to specify these implementation details somewhere so we do so by adding new parameters to QNN or creating new QNN symbolic ops.

2 Likes
#19

I’d like to make sure the end goal of this framework is to create a fully quantized graph, ie with all operators in affine space.

Unlike the usual transformation contraint in TVM that graph rewrite doesn’t change outcome, for quantization, it obviously does. Statistics must be available to help answer how much.

From a BYOC point of view, some group of operators may be replaced by efficient hardware equivalent. For example, conv-add-relu. Also, math functions may be replaced by LUT.

The transformed graph is a simulated quantized graph that allows the user or the quantization framework to always simulate output and handle quantization error. I don’t think we need to provide all combinations but hooks should be in place to allow such custom, user defined, handling.

Finally, the proposal may be missing definition of accumulators in affine space. While weights, inputs (constant or dynamic) and outputs will be in affine space eg int8 dtype, it is important to be able to specify on which dtype intermediate math operations will be, for example int32. If we allow any kind of dtype, then the simulated quantized graph should be able to answer how many bits do I need before saturation. Again, I view such answers as part of statistics the user can analyze. At TIR level, such accumulators may lead to efficient, hardware dependent, transformations.

3 Likes
#20

I apologize for the long delay.

Thanks @electriclilies and team for nicely written RFC. I support the idea. Reading through the comments, it seems that many of us are in agreement about the AutoQ and its reliance on QNN extension. The mentioned pain points mostly revolve around

  • The inconsistency of QNN operators.
  • Wide variety of choices one can make while quantizing a conv2d.

Therefore, to strengthen the integration of AutoQ, QNN and BYOC, we need more consistency in QNN operators. And our auto-quantization algorithm needs to be flexible that it can support different forms of quantization even for the same operator (as @AndrewZhaoLuo mentioned).

The QNN operator inconsistency pain point is interesting and eye opening. I did not know that it was so painful from BYOC perspective. I think it is inevitable that PT/TFLite parsed quantized graphs will have some differences because of the differences in how frameworks support different operators. But, I agree that we must strive to keep it as consistent as possible. I like @masahi idea to add more QNN operators (using automatic code generation maybe) to support operators like resize, pool, relu, softmax.

A question for @electriclilies from the RFC

  1. Extend qnn.conv2d, qnn.dense, etc. to be used with more datatypes, including fp32. We would also have to add an attribute to QNN specify the accumulation datatype used.
  • I am trying to understand why we need qnn.conv2d* (* represents operator along the lines of qnn.simulated_conv2d) during calibration. The only reason would be if you want to propagate the error from previous operators while calibrating current conv2d operator. If we calibrate in a manner that it does not account for the error introduced by quantizing previous operators (common in today’s frameworks), then we need only qnn.simulated_quantize and qnn.simulated_dequantize to calculate the quantization error at the current operator. Is my understanding correct? (Just trying to understand. I will buy the idea that propagating errors while calibration might be helpful for aggressive quantization.)

@electriclilies @mbaret This is somewhat tangential but I wanted to understand more. Suppose, we extend the qnn.conv2d to qnn.conv2d* that supports simulation during calibration. So, we have a pattern, qnn.simulated_quantize → qnn.conv2d* → qnn.simulated_dequantize. What are the input scales and zero points of qnn.conv2d*? IIUC, they should be equal to the qnn.simulated_quantize operator at the inputs of qnn.conv2d*. If that is true, once we finish calibration, can we use this graph for BYOC?