Motivation
Common Subexpression Elimination is a compiler optimization that effectively avoids repeated computation of the same expression. It is needed in the AutoDiff submodule to improve its performance. As an example, consider a compute definition that is as simple as the tanh activation function:
Y = tanh(X)
whose gradient definitions are
dX = (1 - tanh(X) * tanh(X)) * dY
We can clearly see that the value of dX is evaluated for 3 times in this
example: once in the forward pass, and twice in the backward pass. Although such
re-evaluation might not be a big deal here (because tanh is a relatively
lightweight operator), one can probably imagine the trouble that this will bring
as the operators become more complicated, as our examples in the later text will show.
Key Ideas
To illustrate our idea better, we consider the compute definition for the BatchNorm operator and its gradient on the placeholder γ:
![]() ,
,
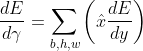
To avoid re-evaluating the normalized x (denoted as x_hat), we must complete the following steps:
-
Analysis
We need to find out that x_hat is the LARGEST common subexpression between the forward and the backward pass.
-
Transform (Forward)
We need to set x_hat as one of the outputs, so that it can be stashed in memory by the forward pass.
-
Transform (Backward)
We need to replace the x_hat in the backward compute definition with a placeholder, whose value will be fed by the one that we stashed in the previous step.
As one might notice, those steps are in essence inferring the feature maps (a.k.a. backward dependency). In legacy machine learning frameworks (e.g., MXNet, TensorFlow) and deep learning libraries (e.g., cuDNN), this is done in a manual, hard-coded way. But here we are doing this automatically, that is, the feature maps are determined in such a way that the amount of computation needed to evaluate the backward gradients is minimized.
Implementation Details
To implement CSE, we need to go through the following steps:
-
Tensor AutoInliner
The tensor inliner is needed to simplify the tensor expressions generated by the AD pass and has already been implemented as part of
autodiff/ad_util. As an example, consider the raw compute definition from the AD pass on the γ gradient of the BatchNorm operator:extracted_tensor[b, h, w, -c] = (X[b, -c, h, w] - E_X[-c]) / sqrt(VAR_X[-c] + ε) dγ[c] += dY[b, c, h, w] × extracted_tensor[b, h, w, -c]As we can see, the introduction of the intermediate tensor
extracted_tensorcauses trouble in the optimization: not only does it have a different indexing order from X (and dY), but a reverse index as well (i.e., c). Futhermore, the access to theextracted_tensoradds an extra level of indirection in the tensor expression comparison (described later). Therefore, the first step of the CSE is to automatically inline all the injective computes in their respective consumers. -
CSE Optimizer
// Note that for simplicity, some low-level details are omitted here. class CSEOptimizer { private: Tensor* src_; TensorExpTree src_tensor_expr_tree_, tgt_tensor_expr_tree_; //< described later private: /// @brief Optimize the expression (to a placeholder) if /// /// src_tensor_expr_tree_.Find(tgt_tensor_expr_tree_.at(expr)) /// /// Dispatch to the following operation nodes: /// - Call /// - +, -, *, / /// - Reduce /// - Int/FloatImm Expr Optimize(const Expr& expr); public: void Optimize(Tensor* const src, Tensor* const tgt) { src_tensor_tree_.Visit(*src); tgt_tensor_tree_.Visit(*tgt); new_body_stmt = Optimize(tgt->op->body); *tgt = ComputeOpNode::make(new_body_stmt, ...); } };The CSE optimizer is constructed from a
srctensor expression to optimizetgt. It stores internally a tensor expression tree for each of them (described later). The optimizer operates on the body statement of target. As it optimizes for each expression, it looks the expression up in the target expression tree for the expression subtree and will replace the expression with a placeholder if the source expression tree is able to locate the same subtree. -
Tensor Expression Tree
class TensorExprTree { private: /*! \brief Construct a tensor expression, whose operator type is \p node * and shape is \p axis. * * Dispatch to the following operation nodes: * - Call * - ProducerLoad * - +, -, *, / * - Reduce * - Int/FloatImm */ TensorExprPtr Construct(const ObjectRef& node, const Array<IterVar>& axis) public: /*! \brief Visit `tensor`'s body statement to construct the expression tree. */ void Visit(const Tensor& tensor); /*! \brief Find a tensor expression in the tree. */ bool Find(const TensorExpr& expr) const; };The tensor expression tree, constructed from a tensor, is a tree-like structure that is used to represent the expressions that a tensor has evaluated. It is in fact very similar to the legacy NNVM graph. The tree is able to search its subtrees to determine if they match certain tensor expression, which, as we have shown earlier, is used by the CSE optimization.